Budoucnost společnosti do značný míry závisí na stupni vzdělání, který získaji nový přírůstky do tý společnosti, tj. děti. Pod pojmem “vzdělání” tu nemyslim to, co do vás nahustí indoktrinátoři v rámci školní docházky. Že jste chodili do školy, ještě neznamená, že jste vzdělaní, i když jste dostali samý jedničky. Pod pojmem “vzdělání” mám na mysli skutečný znalosti, vědomosti a schopnosti, včetně schopnosti myslet, řešit problémy, a podobně. Jestli tohle ve škole můžete získat nebo ne, bude záviset na tom, kdo rozhoduje o školních osnovách.
Když vzdělávací systém za něco stojí, děti se učí a rozvíjeji, a pak můžou fungovat jako užitečná součást společnosti, něčim přispívat, a zároveň se vyvíjet dál a růst ve všech možnejch směrech. Když vzdělávací systém ovládnou dementi, vyroste generace debilů, která je stejně k ničemu jako politici, a všechno jde do sraček.
Když vzdělávací systém ovládnou psychopati a do čela se dostanou Propagandalf a Indoktrinity, stane se samozřejmě nástrojem propagandy a indoktrinace, a vyroste nám generace skládající se z dalších psychopatů, kteří se dostanou do čela a pokračujou v psychopatickejch agendách, zombíků bez samostatnýho myšlení, kteří budou dělat cokoliv se jim řekne, a nervních a vystresovanejch lidí, kterejm se tenhle systém sice nelíbí, ale nevědí, co s tim dělat.
A když vzdělávací systém ovládnou psychopati a dementi zároveň, dostaneme se tam, kde jsme dnes. Myslet se ve škole nenaučí nikdo – naopak, samostatný myšlení je systematicky ničený. Víc energie se věnuje hustění do dětí, jak jsou Ukrajinci nejlepší, spolu s úchylama všeho druhu, než aby se děti pořádně naučily číst, počítat, a věděly něco o světě, ve kterym žijou.
K tomu se váže i téma “povinnosti” školní docházky. Kdyby byl náš školskej systém opravdu o vzdělání, nebyl by žádnej důvod, proč by měl bejt povinnej. Lidi se obvykle vzdělávat chtěji, a když ne, tak neni žádnej důvod je k tomu nutit. Povinnádocházka existuje proto, že systém nechce, aby tu mezi náma mohli pobíhat lidi, kterejm se nedostalo stejný indoktrinace jako všem ostatním, nebo se jim nedej bože dokonce dostalo nějakýho opravdovýho vzdělání. To by byla pro systém velká hrozba.
Vůbec posedlost čímkoliv povinným je neklamnou známkou systému STS (Service to Self). Cokoliv, co je povinný, vždycky prospívá těm, kdo to nařizujou, a ne těm, kterejm je to nařizováno. Kecy o tom, že to musí bejt povinný, aby děti našly v životě uplatnění, jen zrazujou samy sebe. Pokud je to “vzdělání” nutný k uplatnění, tak tim spíš neni třeba to nařizovat, ne? Chceš uplatnění – vzdělávej se. Nechceš – trhni si. Tvoje volba.
Tady se nám v podstatě tvrdí, že je povinný i najít si to “uplatnění”, což v rámci psychopatickýho systému dává smysl, neboť “uplatnění” v tejhle společnosti znamená víceméně “příležitost” dřít jak dement od rána do večera, aby si člověk vydělal na právo existovat, a zároveň byl celej den dostatečně “zaměstnanej” na to, aby neměl čas o něčem přemejšlet a podkopávat tak parazitickej systém nad sebou. A na tenhle život otroctví je třeba připravit děti už ve škole, neboli pořádně jim vymejt mozky a namlátit do nich všechny ty “pravidla” důležitý pro správnej život otroka.
V obzvlášť prohnilej a dementní společnosti to pak jde ještě o pár kroků dál a dětem se vnucuje, že by si měly “změnit pohlaví” (neboli “zmrzačením k trvalej sterilizaci!”), často masturbovat, a aspoň tak od pěti let mít sex, ideálně s několika pedofilníma dospělejma. Člověk by blil. Tyhle extrémy, a politiku ve školách obecně, teď ale probírat nebudeme, ačkoliv se tu na nich pilně pracuje.
Tentokrát se spíš zaměříme na to, nakolik je ten náš “vzdělávací” systém efektivní, neboli nejen jesti se učí to, co je opravdu užitečný, ale hlavně jestli se to, co se učí, učí způsobem, kterej jsou žáci schopni vstřebat a něco si z těch hodin odnýst. Jestli se těm dětem věci vysvětlujou tak, aby to pochopily. Jestli je tu vůbec nějaká snaha o dosažení něčeho, čemu by se dalo říkat vzdělání.
Vycházim z vlastních zkušeností z minulýho století (dneska už naštěstí do školy chodit nemusim a můžu se vzdělávat normálně) a nevim, jak to přesně ve školách vypadá teď – kromě občasnejch hororovejch příkladů v alt.médiích. Vzdělávací systém stál za hovno už v těch 80. letech (a i mnohem dřív), ale z toho, co jsem pochytil, se od tý doby jen podstatně zhoršil.
Pokud jde o to, co se učí, jde to zjevně od desíti k pěti. Ve zdegenerovanym Záchodě zachvátily školství politický agendy švábů a jinejch škůdců, zatímco schopnost číst a počítat pomalu ale jistě klesá, a děti se učí, že kdyby něco potřebovaly, tak si to najdou na Internetu, takže vlastně nemusí nic vědět, a už vůbec ne umět. Proč ty školy teda vůbec máme?
Tohle je samozřejmě perfektní způsob, jak vychovat generaci neschopnejch a nesamostatnejch debilů, kteří budou poslouchat vládu a dělat, co jim přikáže. Ideální závislí otroci. Zároveň tuhle generaci můžete lusknutím prstů degradovat pod úroveň jeskynních pralidí, když jim vypnete proud. Bez mobilu a Internetu si ani nedojdou na záchod.
Kdo projde takovym “vzdělávacím” systémem, bez elektroniky nikam netrefí, pěšky nikam nedojde, neumí nic vyrobit nebo ani opravit píchlou duši u kola, a obecně se ztratí v ten moment, kdy přestane fungovat elektřina, a nebude tušit, co dělat. Neboli vzdělání v pravym slova smyslu nemá prakticky žádný. “Ví” jen, že si může každej den vybrat, ke kterýmu z 999 pohlaví se bude hlásit, a že Ukrajina je nejlepší demokracie na světě (která předčila dokonce i Izrael), ale nerozezná ostruhy od ostružin a erupce or korupce.
Jiná otázka je, jak se učí. Neboli když vezmeme ty věci, který k něčemu jsou a ještě je ve školách (snad) úplně nezrušili, jako matematika nebo historie, tak jestli se daří v dětech vůbec vyvolat o to vzdělání nějakej zájem, jestli je jim to podáváno způsobem, kterej jsou schopny pochopit, a jestli v nich po ukončení tohodle povinnýho utrpení nějaký to vzdělání zůstane.
Jak se učí
Zástupci škol často tvrdí, že jejich škola podporuje samostatný myšlení (nebo to teda aspoň říkali tenkrát – možná už se dneska ani to nesmí). Jakožto někdo, kdo nikdy neměl moc tendenci jít s davem, jsem nikdy nepociťoval, že by tohle tvrzení bylo pravdivý. V podstatě kdykoliv měl člověk na něco jinej názor než vyučující, konečnej výsledek byl, že jestli chcete mít dobrý známky, tak se budete držet toho, co říká vyučující. Samostatně myslet můžete, ale budete za to mít horší známky (případně tresty). To mi nepřipadá jako “podpora” samostatnýho myšlení.
A rozhodně se běžně nestávalo, že by nás někdo učil samostatně myslet. K tomu mohlo dojít leda tak když měl někdo velký štěstí a narazil na jednoho dobrýho učitele, kterej měl zdravej rozum, školní osnovy tak moc nežral, a opravdu měl zájem na tom, aby se děti vzdělaly. Takovejch případů ale moc nebylo. (Dneska jsou udáni, vyhozeni z práce a trestně stíháni.)
Převážně se vyžadovalo, abysme se naučili nazpaměť, co se nám nadiktovalo, a uměli to zopakovat (a někdy byl průser i to, že jsme to nedokázali zopakovat dostatečně doslovně), případně abysme se naučili určitý metody (jako v matematice) a používali jen tyhle schválený metody. Pamatuju si velmi dobře, jak byl vždycky problém, když někdo napsal na konec matematický rovnice správnej výsledek, ale neměl tam popsanou “správnou” metodu.
V podstatě i když jste měli správnej výsledek, odpověď mohla bejt považovaná za nesprávnou. Což je evidentně na hlavu. Tenkrát nám to připadalo jen jako otrava a nespravedlnost, ale když se na to člověk teď podívá zpětně, může se po desítkách let zkušeností právem pozastavit nad tim, proč se vyžadovala konkrétní metoda, který se všichni museli držet.
Přitom k výsledku se dá dojít i jinejma metodama, k čemuž se ještě vrátíme, a kromě toho jsou lidi, kterejm to prostě myslí trochu líp, a ten výsledek jim v hlavě vyskočí okamžitě, aniž by se museli zdržovat nějakou blbou “metodou”, kterou se jim nevrlej učitel snaží naordinovat. Takoví žáci věděli výsledek hned, a pak museli přemejšlet, “Eh, jak byla ta kretenská metoda, co tady musim napsat, abych dostal jedničku?” (Neboli ti chytří se museli naučit imitovat ty blbý!)
Na takovejch příkladech je vidět, že školství neni o vzdělání, ale o určitej “standardizaci” toho, co lidi ví a jak k čemu přistupujou. Nevychovává se množství unikátních jedinců s odlišnejma silnejma stránkama a schopnostma, ale uniformní masa otroků, která zná stejný věci a všechno dělá stejně.
Zopakuj mi, co jsem ti řekla, a dostaneš jedničku
Sice nám věčně někdo tvrdil, že známky nejsou tak důležitý a že se učíme pro ty vědomosti, ale zároveň v praxi všechno fungovalo tak, že ty známky důležitý byly. Paradoxně to v některejch směrech měli lepší žáci se špatnejma známkama, protože jejich rodiče si zvykli, že jsou to prostě blbové, a žádný zázraky od nich nečekali, zatímco někteří z nás byli doma běžně seřváni za dvojku, a za trojku už někdo třeba dostal i přes držku. Ale o známky nešlo, to ne.
Co bylo zapotřebí, aby člověk dostal ty jedničky? Umět samostatně myslet? Velký kulový. Museli jste správně zopakovat, co nám někdo nadiktoval. Nebylo ani třeba něco z toho chápat. Když jste ze sebe vysypali něco, co jste sice vůbec nechápali, ale podařilo se vám to správně odrecitovat, bylo to “dobře”. Když jste situaci chápali, někdy i líp než ten učitel, ale neprezentovali jste to dostatečně podobnym způsobem, jakym vám to bylo předáno, bylo to špatně.
Totální průser byl, když látku vyučoval někdo, kdo jí sám pořádně nerozuměl. Takový případy pak obzvlášť sralo, když tomu někdo z dětí rozuměl líp a nedej bože to ještě dával najevo, takže pak ti nejlepší mohli trpět nejvíc. Super “vzdělávací” systém, ne?
Opakování nazpaměť naučenýho materiálu zabíjí myšlení. Učíte se opakovat, ale ničemu z toho nerozumíte. Navíc jste nuceni opakovat spoustu věcí, který ani nejsou pravda, což je podstata indoktrinace – naučit vás ty lži opakovat tak bezmyšlenkovitě, že by vás ani nenapadlo zamyslet se nad tim, že by to mohlo bejt jinak. To se parazitům náramně hodí později – v dospělosti pak nezpochybňujete žvásty politiků, protože jste zvyklí poslouchat a opakovat a nepřemejšlet.
Opakování neni matka moudrosti. V opakování žádná moudrost neni. Opakování je základ propagandy.
Jak už jsem jednou někde zmiňoval, pamatuju si ze školy “1620 – bitva na Bílej Hoře”. Jenže to je všechno, co o tom vim. (Navzdory tomu, co by si čtenáři Antiviru mohli myslet, historie mě ve škole nikdy nebavila, právě z toho důvodu, jak byla vyučovaná.) Nevim kdo v tej bitvě bojoval a s kym a proč a jak to dopadlo. Jen datum a název bitvy, jak to po mě soudruzi a soudružky chtěli/y.
Nebylo by z praktickýho hlediska lepší vědět, proč se bojovalo a že to bylo “nějaký stovky let zpátky”? Jestli to bylo 1620 nebo 1630 je úplně jedno. Stačí vědět, že to bylo pár set let zpátky a ne ve starověku nebo předloni. Jaká je pointa toho, znát datum bitvy, když se nepodařilo do mě dostat, o čem ta bitva byla? Co jsem se takhle opravdu naučil užitečnýho? Vůbec nic.
Dějepis ve škole byl špatnej vtip. Probíhala tam jakási destrukce kontextu. Byly to jen oddělený letopočty, bitvy, války, povstání, a podobně. S tim, jak nám to bylo podáváno, jsem v tom nikdy neviděl nějaký souvislosti nebo smysl. A proto mě to nebavilo a nic jsem se z toho nenaučil. Veškerý moje znalosti o historii pochází z knížek, který jsem čet z vlastní iniciativy, a ne ze školy.
Jelikož se učitelé nesnažili o to, abych tu historii chápal jako nějakej celek, kterej nás učí něco o tom, jak funguje lidská společnost, ale o to, abych si pamatoval datumy a názvy bitev, tak vim jen “1620 Bílá Hora”, což je naprosto nepoužitelná informace. To už byly víc vzdělávací večerníčky.
Do kontrastu s tim si můžeme dát 11.9.2001 – o tom bych moh bez problémů napsat celou knížku, protože to jsem si nastudoval sám. Jen za velmi málo z toho, co dnes vim, můžu dát nějakej kredit škole. Naopak jsem musel strávit ohromný množství času studováním toho, jak je to opravdu s věcma, o kterejch nám ve škole lhali. A těch bylo hodně. V podstatě asi většina.
Čísla
Specifická oblast, u který se tu zastavim, jsou čísla a matematika. Je to takovej dost vyhraněnej předmět, kterej někteří měli rádi, protože tam nemuseli skoro nic dělat, zatímco ostatní ho nesnášeli, protože ho nechápali a nešlo jim to. Je hodně lidí, kteří si o sobě myslí, že na matematiku jsou prostě “blbí” a smířili se s tim, že jakýkoliv matematický problémy přenechávaji někomu jinýmu. Podle mě je to ale u mnoha z nich jen výsledek špatnýho učení.
Já jsem patřil mezi ty, kterejm čísla prostě vždycky dávaly smysl a naučit se cokoliv v matematice nikdy nebyl problém. Z nějakýho důvodu si líp pamatuju dlouhý čísla než jména a tváře lidí. Když si vyzvedávám zboží v Alze, nadiktuju jim to devítimístný číslo objednávky zpaměti a oni na mě zíraji, jaktože to odnikud nečtu. Přitom mi to zapamatování trvá jen pár vteřin. Prostě to máme v tej hlavě každej nastavený jinak. Mně se zas lidi někdy musí představit třikrát, než si to zapamatuju.
Takže někdo má na čísla nějakej talent a někdo ne, a kdo ne, pro toho je ten školní systém těžko pochopitelnej. Že někdo projde školu s tim, že “na matematiku neni”, ja ale podle mě víc chybou tý školy než jeho. Ten člověk by to podle mě většinou pochopil, kdyby se mu to vysvětlilo nějak jinak, ale škola má na všechno jen jednu předepsanou metodu, a když ji někdo nechápe, tak ta škola si s tim prostě neporadí a ten člověk se to nikdy nenaučí. Nikdo mu to nedokázal vysvětlit tak, aby mu to dávalo smysl. Aby si to dokázal představit. Tohle mám i trochu ověřený v praxi.
Kdysi jsme v práci řešili nějakej celkem triviální problém a jedna kolegyně rezignovaně řekla, “tohle po mně nechtějte – já jsem na matematiku blbá”. A prostě vzala na vědomí, že tohle ona rozhodně nevyřeší. Ten problém byl ale dost jednoduchej a kolegyně mi nepřipadala tak blbá, že by to nepochopila, tak jsem si řek, že jí to vysvětlim.
Po dvou minutách na mě valila oči a říkala, “Ty vole, proč mi to takhle nevysvětlili ve škole? Takhle to chápu! Vždyť je to úplně jednoduchý!” A tak v nějakejch 40 letech zjistila, že neni “blbá na matematiku”, ale problém je někde jinde. Jenže školy si jedou svým rigidním stylem, a spousta dětí nedostane šanci rozvinout potenciál, kterej ve skutečnosti maji, a pak si celej život myslí, že jsou na to “hloupý”.
Pokud patříte mezi lidi, kterejm čísla nevoní a radši se jim vyhybáte, pokusim se vám je tu ukázat trochu jinak. Částí toho školního problému je, že se něco vysvětluje 30 dětem zároveň. Matematiku musíte chápat postupně od toho jednoduššího ke složitějšímu. Když přeskočíte dvě kapitoly v hostorii, je to celkem jedno. Když nezvládnete v matematice základy, tak jste skončili. Vysvětlující by teda měl s žákem neustále kontrolovat, jestli pořád ještě chápe, protože když ne, tak nemá smysl pokračovat.
Tenhle problém se ve škole moc neřeší. Jsou lepší vyučující, kteří se snaží s dětma nějak normálně kominukovat. Bohužel jsou tam ale taky takový ty rigidní autoritářský struktury, který děti neustále okřikujou a nestrpí, aby se při hodině ze třídy ozvalo jediný slovo. Potom i když se náhodou zeptá, jestli všichni chápou, nikdo z těch nechápajících se radši nehlásí, i když jich je 25. Nemluvě o tom, že introverti vůbec nemaji zájem se ve třídě 30 dětí hlásit a něco říkat, obzvlášť když to je “já to nechápu”, a obzvlášť před protivnym učitelem. Na to ale školy nemaji řešení.
To je ale jen jeden z problémů. Pak je tu třeba to, že pro spoustu lidí jsou čísla něco abstraktního, co si nedokážou pořádně představit. A obávám se, že někteří vyučující na tom nejsou líp, takže nemá kdo to tomu dítěti nějak přiblížit. To se nejdřív musí naučit řadu znaků:
1 2 3 4 5 6 7 8 9 10
To jsou ale pro dítě nic neříkající symboly, který se nijak nevztahujou ke skutečnýmu světu. Ten symbol pro sedmičku nijak neřiká nic o tom, co reprezentuje. Mnohem líp by si ty čísla to dítě představilo třeba takhle:
. : .: :: .:: ::: .::: :::: .:::: :::::
Každej znak takhle jasně ukazuje, co znamená. Číslici by si člověk měl představovat ne jako nějakej klikyhák, kterej jinak nic neznamená, ale jako něco, co v sobě obsahuje tu hodnotu, kterou reprezentuje. Pak už je tu velkej rozdíl třeba ve sčítání:
3 + 4 = ?
Tady neni nijak patrný, že výsledek je 7. Aby to člověk sečet, musí “vidět” tu hodnotu těch tří a čtyř. Nevim sice, co se děje v hlavách antimatematiků, ale mám takový obavy, že se to sčítání někteří taky učí “nazpaměť”. Když si to ale napíšeme takhle, tak je výsledek evidentní:
.: + :: = .:::
Pro nějaký efektivní sčítání a odčítání by si měl člověk bejt schopnej představit ty čísla jako něco reálnýho, a ne jen jako abstraktní symboly. Když sčítáte 5 a 7, je blbost “pamatovat si”, že 5 a 7 je 12. 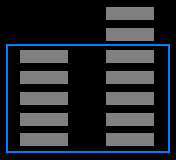 Jestli jste se to naučili takhle, měli byste asi zažalovat tu školu. Sice čím víc si toho pamatujete, tím líp pro vás, ale matematika neni o paměti. Je o logice a schopnosti si to vizualizovat a věci si odvodit.
Jestli jste se to naučili takhle, měli byste asi zažalovat tu školu. Sice čím víc si toho pamatujete, tím líp pro vás, ale matematika neni o paměti. Je o logice a schopnosti si to vizualizovat a věci si odvodit.
Místo toho si teda můžete představit třeba stoh 5 mincí a vedle něj stoh 7 mincí a celý si to vizualizovat. Když si to představíte takhle, “vidíte” v tom snadno desítku a dvojku (viz obrázek) a výsledek je patrnej na první pohled. Komu z vás ale učitel ve škole dal ty čísla do nějaký souvislosti s realitou? Možná jste začínali s počítáním na prstech, ale to je asi tak všechno.
Jelikož používáme desítkovou soustavu, je dobrý vědět, z čeho se ta desítka skládá, neboli dobře znát všechny varianty, na co se dá rozložit, nebo ještě jinými slovy, který dvě číslice jsou komplementární, tj.: 1+9 | 2+8 | 3+7 | 4+6 | 5+5
To se asi nazpaměť naučíte, ale opět si to můžete představit i nějak takhle:
. + ·:::: | : + :::: | :. + ·::: | :: + ::: | ::. + ·::
a vidíte, že všechny ty dvojice tvoří tu desítku.
Na desítkovou soustavu jsme zvyklí, tudíž s desítkama se nám počítá mnohem líp než s osmičkama nebo dvanáctkama. Líp se vám počítá 10+9 než 8+9 nebo 12+9. Početní operace se potom daji přerovnat nebo zredukovat do nějaký srozumitelnější/jednodušší podoby.
Například máte spočítat 23+9. (Tohle jsou samozřejmě jednoduchý příklady, se kterejma asi nikdo pomoc nepotřebuje, ale jde tu o principy, který se pak daji uplatnit i u složitějších operací.) Co tady udělám jako první, je, že si tu trojku a devítku prohodim, takže mám 29+3. Nevim jak vy, ale já tady u tý druhý varianty ten výsledek vidim mnohem jasnějc.
Když to rozeberu, tak jde o to převádení na desítky. To se děje víceméně vizuálně. Můžeme si to představit jako ty mince – stoh 23 mincí a stoh 9, s tim, že 10 mincí si představíme zabalenejch do nějaký krabičky a tu bereme jako větší celek. Takže máme vizuálně dvě krabičky a na nich 3 mince a vedle 9 mincí.
Když to prohodíme, máme na jednej straně 29 mincí a víme, že už nám zbejvá jen jedna, abysme měli 3 krabičky. Na druhej straně máme 3 mince, takže z nich vezmem jednu, kterou doplníme ten první stoh do 30 a zbydou nám dvě. Pak máme 30+2 a to už je jasný. Takže se to proháže 23+9 → 29+3 → 30+2. Když si to představujete vizuálně, všechno to snadno dává smysl a proběhne to velice rychle.
Podobně když potřebujete sečíst 86+93, můžete si tu trojku přidat k tej šestce – 89+90, a ještě lépe to hodit do tý devadesátky – 99+80. Takhle se na jednej straně dostanete těsně pod stovku a víte, že výsledek je 180 bez jedný. Takovýhle přesunování nám může ve vyšších číslech problém o dost zjednodušit.
Bohužel spousta lidí vylezla ze školy se dvěma sadama matematickejch problémů – těma, co si pamatujou nazpaměť, a těma, který nespočítaj. A mysleji si, že na tu druhou sadu jsou moc hloupí, protože jim nikdy nikdo neukázal žádnou metodu, jak se snadno dobrat výsledku.
Násobilka “po Japonsku”
Tady u nás a v kolektivním Záchodě se učí násobit “pod sebe”. Ne všude se to ale dělá stejně. Třeba v Japonsku se děti učí jinou metodu, která vypadá takhle:
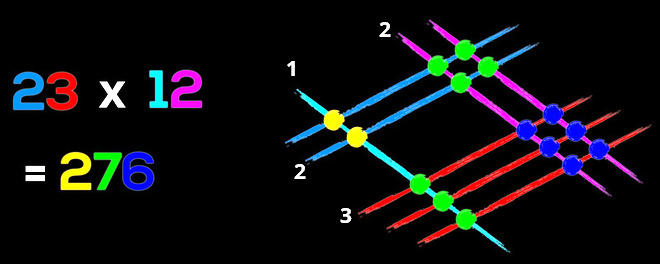
12 nakreslíte jako 1 čáru a 2 čáry, 23 pak přes ně jako 2 čáry a 3 čáry. Vlevo se vám to protne 2x, uprostřed 7x (4 nahoře, 3 dole) a vpravo 6x. Výsledek je teda 276. Když lidi z kolektivního Záchodu na tuhle metodu někdy ve 40 letech náhodou narazí, často kroutí hlavou nad tim, proč se to učili ve škole tou naší trapnou metodou a ne touhle, protože tahle jim připadá lepší.
O tom, která metoda je lepší, se dá debatovat, a možná každýmu sedí jiná, ale pointa je – kolik z vás o tejhle japonskej metodě někdy slyšelo? A komu z vás o ní řekli ve škole? Nejspíš nikomu.
Proč? Je možný, že by o ní ve většině světa nevěděli? Neni. Obzvlášť v dnešní době. Proč se teda rozhodli to všechny učit jen jednou metodou a tu od všech vyžadovat, když si hodně lidí myslí, že ta druhá je lepší? Nedávalo by smysl ukázat dětem obě a nechat je, ať si vyberou, kterou chtěji? Hlavní je, aby došli ke správnýmu výsledku, ne?
Ale ani v tom tady neni pořádná svoboda. Žádnej výběr nebude! Prostě vám nadiktujou, jak to máte počítat, a o jinej metodě vám ani neřeknou, natož aby vám ji dovolili používat.

Na větších číslech to pak vypadá například takhle. Jedničku z tý 14-ky připočtete k tej osmičce nalevo. Efektivita týhle metody samozřejmě klesá s vyššíma číslicema. Násobením 286×927 byste počmárali celej papír. Na druhou stranu, při potřebě bez kalkulačky vynásobit 286×927 by většina lidí stejně utekla, a kdyby jim šlo o život a museli to spočítat, možná by to čmárání po celym papíře přece jenom bylo jistější, protože je tam i menší šance, že uděláte chybu. Líp se v tom orientujete.
Hlavně je tu ale to, že tahle metoda vám vizuálně ukazuje, jak to násobení vlastně funguje. Vidíte názorně, jak se tam organizujou ty jedničky, desítky, stovky, atd. I když nakonec skončíte s násobením “pod sebe”, tahle metoda vám líp objasní, jak ty čísla fungujou.
Pokud jde o efektivitu učení, dává rozhodně smysl naučit děti co nejvíc možností, jak se něco dá udělat, a nechat je vybrat si ten způsob, kterej jim vyhovuje. Naordinovat všem jeden jedinej způsob rozhodně efektivní neni, a zatajit jim všechno ostatní už pomalu hraničí se zločinem. Dá se takhle věřit, že školám jde o vzdělání?
Zamyslíme-li se nad tim, že každej je jinej a myslí mu to trochu jinak, tak pro některý lidi prostě ty vybraný metody jsou úplně nepoužitelný, protože jim to nedává žádnej smysl, a ten člověk je pak diskriminovanej na celej život, protože něco “neumí”, a to jen z toho důvodu, že mu předhodili jen jednu metodu, která mu zrovna vůbec neseděla.
Z celýho toho systému, kde se ke každýmu problému předepisuje jen jeden způsob řešení, maji potom všichni hrozně rigidní myšlení, který vůbec neni samostatný. Člověk si poradí jen s tim, s čim ho ve škole naučili si poradit. Rozděluje věci na “to umim” a “to neumim”. A když “to neumim”, tak se vůbec nesnažim si s tim nějak poradit. Prostě neumim. Konec. Problém někoho jinýho.
Kategorie “to neumim” by ale prakticky neměla existovat. Místo ní by tam měla bejt kategorie “to sice v tuhle chvíli nevim, jak vyřešit, ale když o tom trochu popřemejšlim, tak určitě na něco přijdu”. Takovej způsob myšlení se ale ve školách nepředkládá. “Tady máš problém, tady metodu, a ukaž nám, žes to vyřešil přesně tak, jak jsme po tobě chtěli.” Příkazy, zákazy, žádný samostatný myšlení. Jako drezura.
Je to nějaká systemická nekompetence, nebo je to účel? Samozřejmě to žádná náhoda neni. Tohle vytváří takový lidi, jaký systém parazitů potřebuje – ne moc chytrý, předvídatelný, a co nejmíň samostatný a co nejvíc závislý na autoritách a jejich instrukcích. To, že pak většina lidí skočí na falešný pandemie a podobně, začíná už ve škole a v tom, jak se učí.
Tady máme příklad čtyř různejch metod, jak spočítat 13×22:
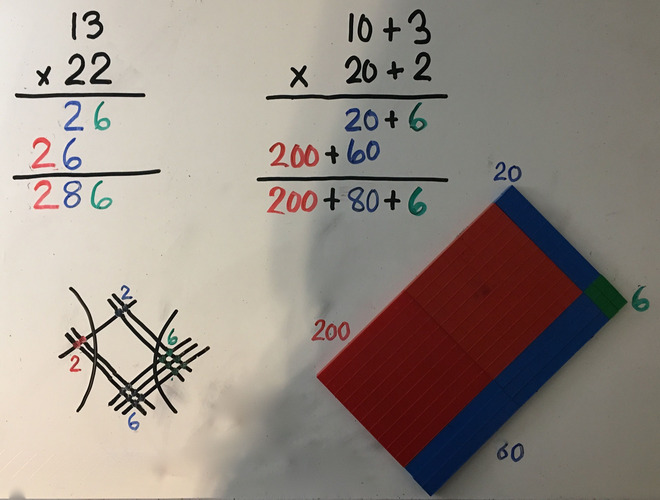
Pro spoustu lidí může jedna z těch metod bejt na první pohled velmi srozumitelná a jiná naprosto neprůhledná. Ve škole vám ale ukážou jen jednu, a když je to zrovna ta pro vás neprůhledná, tak jste pěkně v prdeli.
Osobně bych v tomhle případě nepoužil ani jednu. Dal bych si 10×22 (220) plus 3×22 (66) a sečet 220 a 66. Takže máme pět metod. Ale můžeme jít dál. Můžeme si to zase trochu zpřeházet. Jde tu o násobení, takže když jedno z čísel vynásobim třeba dvěma a to druhý vydělim dvěma, tak mám pořád stejnej problém, ale možná bude přehlednější.
V tomhle případě si můžu 22 vydělit dvěma a dostanu 11, což je dobrý, protože s jedničkama se dobře počítá. Pak si musim 13 vynásobit dvěma a dostanu 26. Místo 13×22 mám teda 26×11, nebo 11×26. Z toho je pak celkem evidentní, že je to 260+26 (10×26 + 1×26). To už se sečte snadno. A máme šestou metodu.
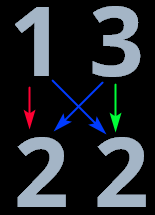 Když počítáme 13×22, můžeme si to rozložit na několik operací. Máme tu 10×20 (neboli desítky z každýho čísla), což nám k výsledku dá stovky, tady teda 200. Máme tu 3×2 (jednotky z každýho čísla), což nám dá 6. A pak je ten střed, kterej nám k výsledku dodá desítky. Tady to musíme zkombinovat křížem a máme tu 10×2 a 3×20. (Nebo 1×2 a 3×2 a přidat ke každýmu nulu.)
Když počítáme 13×22, můžeme si to rozložit na několik operací. Máme tu 10×20 (neboli desítky z každýho čísla), což nám k výsledku dá stovky, tady teda 200. Máme tu 3×2 (jednotky z každýho čísla), což nám dá 6. A pak je ten střed, kterej nám k výsledku dodá desítky. Tady to musíme zkombinovat křížem a máme tu 10×2 a 3×20. (Nebo 1×2 a 3×2 a přidat ke každýmu nulu.)
Na obrázku je červená šipka pro stovky, modrý pro desítky, a zelená pro jednotky. To je základ celý týhle početní operace, kolem kterýho se pak točí ty různý metody. Násobení dvojcifernejch čísel má 4 komponenty, z nichž 2 jsou na stejnej úrovni (modrý šipky).
Když se podíváme nahoru na tu japonskou metodu pro tenhle případ, tak ta červená dvojka odpovídá červenej šipce, modrý čísla modrejm šipkám, a zelená šestka zelenej šipce. A stejný je to i s těma obdélníkama vedle.
Tohle rozdělení podle těch šipek je nám matematikům naprosto jasný a mnozí si asi řikaji, proč takovou kravinu vůbec vysvětluju, ale vsadil bych se, že spousta z těch nematematiků si tohle ani nikdy neuvědomila. Nikdo jim to nevysvětlil, je to nikdy až tak moc nezajímalo, protože ve školním podání je matematika silně nebavila, a všechny ty čísla jsou pro ně jen pěkná otravnost.
Jak ale pak můžou přijít sami na nějaký řešení, pro který nemaji naučenou metodu, když jim ty čísla nic neřikaji, nedokážou si to nijak představit, a to násobení ani neumí rozložit na jeho komponenty? To je docela tragický, ale neni to tragédie těch lidí, ale toho školství.
K výsledku se vždycky dá dojít několika způsoby, a v různejch situacích můžou bejt lepší různý způsoby. Osobně používám různý metody podle toho, jaký mi to zrovna předhodí čísla a co se s tim dá nejlíp dělat. S určitejma číslama se pracuje líp než s jinejma, a od toho se odvíjí i ta metoda. Můžeme si vyzkoušet pár příkladů a jak by se na ně dalo jít.
15×17 – tady neni nic moc, co by mi očividně pomohlo, takže bych na to šel hrubou metodou, tj. rozdělením na ty 4 komponenty, což by byly 10×10, 10×7, 5×10 a 5×7. Jelikož mi ale obě čísla začínaji jedničkou, tak si ty první dva kroky spojim. Budu teda počítat 10×17 + 5×17, a 5×17 si rozdělim na 5×10 a 5×7. Tim pádem mám 170+50+35. Buď to můžu sčítat postupně, nebo když mám takhle ty 3 čísla na sečtení, tak tam vidim, že 7 a 3 mi daji desítku, neboli 170 a 30 mi daji 200. Tu pětku pak přihodim tam nebo tam, takže si to zredukuju na 205+50 nebo 200+55.
Ve svojí hlavě to potom “vidim” nějak takhle, jako takový “krabice” se 170, 50 a 35 kusama čehosi, který jsou velký podle toho, kolik je v nich kusů:
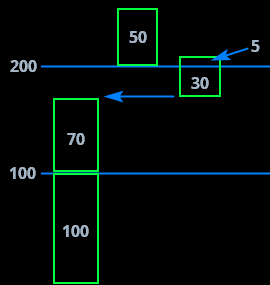
A v hlavě si to vizuálně poskládám, aby to dávalo smysl. Krabici s 35 kusama si posunu nad těch 170, abych si dal dohromady dvě stovky, a pak mám nad čarou s hodnotou 200 pět kusů z tý krabice třiceti pěti a celou tu krabici s 50 kusama. Takže pod čarou mám 200 a nad čarou 50 a 5.
Tim nechci říct, že tohle je nějakej “dobrej” způsob, jak si to vizualizovat – já to tak prostě vidim automaticky, protože v mojí hlavě to dává smysl a pomáhá mi to prakticky si představit, co ty čísla znamenaji. Někomu to může připadat jako blbost; jinýmu to může dávat víc smyslu než jen napsaný čísla, ze kterejch jejich hodnota neni nijak očividná. To počítání a vizualizace se dějou zároveň a doplňujou se.
Pokud to budete počítat na papíře, většinu těch “triků” asi oželíte. Já jsem zvyklej počítat z hlavy, co se dá, a u toho je nejtěžší (aspoň pro mě) udržet v hlavě všechny ty mezivýsledky. Ty “triky” mi buď redukujou počet těch mezivýsledků, co si musim pamatovat, nebo mi dávaji mezivýsledky snadnější na zapamatování.
Dalo by se to spočítat i úplně jinak. 15 je dělitelný třema, tak to vydělíme a máme 5. Sedmnáctku pak musíme třema vynásobit a máme 51. Vypočítat 5×51 je pak celkem snadný, neboť je to 250+5.
42×25 – Tady máme docela dobrý čísla. 42 se dá vydělit dvěma a zároveň vynásobit dvěma, aniž by kterákoliv číslice šla přes desítku. Neboli čtyřku i dvojku můžeme vynásobit zvlášť a nikde se nám nic neposune. Zároveň 25 je 5×5 a taky čtvrtina ze stovky. To se taky může hodit.
Máme teda spoustu možností. 25×42 je jako 2.5×420. Neboli 840 (2×420) plus půlka ze 420, tj. 210. 840+210=1050. Určitě ne ten nejlepší způsob, ale pořád použitelnej.
Můžeme si to taky předělat na 21×50, když si jednu stranu vydělíme dvěma a druhou vynásobíme. 20×50 je 1000, k tomu přidáme 1×50, a máme 1050.
Jelikož z 25 se dá udělat stovka vynásobením čtyřma, stojí za to se zamyslet, jestli je to schůdný, protože stovkou se násobí snadno. Museli bysme 42 vydělit čtyřma. Čtyřicítka jde skvěle, ale z tý dvojky by nám zbyla půlka. To obvykle neni moc praktický, ale když budeme násobit stovkou, tak je to v pohodě. Máme pak 10.5×100 a z toho opět snadno dáme dohromady 1050.
Ještě jiná možnost by byla rozdělit si to na 42x5x5, z čehož dostaneme 210×5, což jde taky celkem snadno. Pointa je, že když se člověk naučí o tom přemejšlet trochu jinak a vidět ty čísla jako něco víc než jen čmáranice na papíře, často se naskytnou snadný řešení, který by se s použitím jedný metody nikdy neobjevily.
 59×33 – U čísel končících devítkou je někdy užitečný o nich uvažovat jako o 10-1. Násobilka devíti má takovou jednu hezkou vlastnost. Kolik je 1×9 ví každej, a 10×9 taky. Co ten zbytek? Když si ty rovnice napíšete pod sebe, stačí to projet odshora dolu a napsat čísla od 1 do 8, a pak to vzít od 1 do 8 zase odspoda nahoru.
59×33 – U čísel končících devítkou je někdy užitečný o nich uvažovat jako o 10-1. Násobilka devíti má takovou jednu hezkou vlastnost. Kolik je 1×9 ví každej, a 10×9 taky. Co ten zbytek? Když si ty rovnice napíšete pod sebe, stačí to projet odshora dolu a napsat čísla od 1 do 8, a pak to vzít od 1 do 8 zase odspoda nahoru.
Zároveň když na tom obrázku v každym řádku sečteme to oranžový a modrý číslo, dá to dohromady 9. Jo, matematika je takhle celkem zábavná, když vám ji ve škole blbě neznechutí nějaká parodie na učitele.
Když přičítáme devítku, je to jako přičíst desítku a odebrat jedničku, a podobně při násobení devítkou je to jako násobit deseti a pak tu hodnotu násobenýho číslajednou odečíst. Což se v praxi často hodí.
V případě 59×33 se nám na to teda asi nejlíp půjde, když 33 vynásobíme 60ti a pak odečteme 33. (Neboli místo 59×33 je to 60x33-1x33.)
Násobíme tu teda 30×60 a 3×60, a potom odečteme 33. 1800+180=1980. 1980-33=1947. (Nějak jsme se dostali přes ilumináty do Roswellu…)
Jelikož odčítání a dělení jsou podstatně větší opruz než sčítání a násobení, to 80-33 obvykle dělám na dvakrát, tj. 80-30=50, 50-3=47. Jinak mám ve složitějších případech tendenci se občas o desítku seknout. Každopádně 60×33-33 je podle mě o dost jednodušší úkol než 59×33 klasickou metodou. (Místo dvou čísel, 5 a 9, násobíte jen jednim, 6.)
Tenhle princip se někdy dá rozšířit i trochu dál. Třeba 2×96 můžeme počítat normálně, tj. 180+12. Zároveň ale na první pohled vidíme, že výsledek bude “něco pod dvě stovky”. Kolik bude do těch dvou stovek zbejvat? Násobíme dvěma, takže dvakrát tolik, co chybí do sta u tý 96ky, což jsou 4. Takže je to 200-8, neboli dvakrát 100-4.
Zajímavý jsou určitý konkrétní operace, jako násobení čísla končícího na pětku sebou samotnym, tj. například 25×25. Tohle jde strašně jednoduše. 25 je mezi 20 a 30. Takže vynásobíte 2×3, tj. 6, a připíšete za to 25 → 625. Na konci je vždycky 25, protože to je 5 na druhou. Takže 35×35: 35 je mezi 30 a 40. 3×4=12. Za dvanáctku napíšeme 25 → 1225.
45×45 → 4×5=20 → 2025.
55×55 → 5×6=30 → 3025.
65×65 → 6×7=42 → 4225.
75×75 → 7×8=56 → 5625.
atd.
Podobně se daji násobit dvě za sebou jdoucí čísla s pětkou na konci, jako 35×45. Tady uprostřed mezi nima je 40. 40 na druhou je 1600. Tentokrát tu 25ku odečteme a dostaneme 1575. Všechny takový výpočty končí na 75. Když si zkusíme 65*75, tak střed je 70, 70×70=4900, bez 25 je 4875.
A je toho samozřejmě mnohem víc. Kdo z vás o tom všem slyšel něco ve škole?
Když to shrnu, tak je dobrý si ty čísla vizualizovat jako něco, co si člověk dokáže představit (stohy mincí, krabice), prozkoumat víc metod než jen tu jednu ze školy, a ty výpočty si zjednodušit nějakou redukcí.
Když ty čísla vnímáte jako něco, co se dá spočítat tim, že na to koukáte, dává to všechno víc smyslu. Podle toho, jak je pro vás nejlepší si to vizualizovat, si najdete nejvhodnější metodu. A většina početních operací se dá nějak zjednodušit na přehlednější variantu.
Dobrý jsou čísla, který maji hodně dělitelů. 15×16 si můžete změnit na 30×8, 60×4, 5×48, atd. 5×48 se dá spočítat jako 5×50-10. 83+19 se dá vzít jako 83+20, tj. 103 a ubrat jedničku, což bude asi jednodušší než posčítávat všechny ty jednotlivý části. 123+219 se dá změnit na přehlednější 122+220 nebo 120+222.
O tom všem vám toho ale náš neefektivní vzdělávací systém moc neřekne.
Jak si pamatovat čísla
Když se s číslama zachází jako s něčim abstraktním, je těžký si je pamatovat. Pro spoustu lidí je představa, že by si do zejtřka měli zapamatovat číslo 77593754, děsivá. Pokud nebudou pod pohrůžkou smrti, tak se o něco takovýho vůbec nebudou pokoušet. Nebudou mít tušení, jak na to, a nejspíš se budou snažit si ho řikat pořád dokola a doufat, že to v tej hlavě zůstane. To neni moc efektivní metoda. A pokud si dobře pamatuju, na něco takovýho nás ve škole neučili vůbec nic.
OK, je to ale vážně tak strašnej úkol? Jak na to můžeme jít, aby to nevypadalo tak hrozně?

Situace bude vypadat mnohem příznivějc, když si to napíšeme například takhle. Teď už v podstatě stačí zapamatovat si pět-devět-tři / pět-čtyři, a ty sedmičky si budete pamatovat vizuálně, že před první pětkou jsou dvě a před druhou jedna.
Zkusim do klávesnice nabouchat další náhodný 8-místný číslo… 29870753. Co s tim? Tady už tak jasnej vzorec nevidíme. Způsobů je ale mnoho, tak jen zkusíme nějakej jinej. Jestli máte před sebou normální počítačovou klávesnici, s tou číselnou částí napravo, napište si to číslo na ní a sledujte, co dělaji vaše prsty.
Něco se nám tam objevilo, že? (Mimochodem, psal jsem to náhodně na těch normálních číslech nad písmenama, takže tohle nebyl záměr.) Zjistili jsme, že 987 máme v řadě a 753 máme v řadě diagonálně. Neboli si potřebujeme zapamatovat: dvojka, pak horní řada zprava doleva, nula, pak diagonála z levýho horního rohu doprava dolu. To už nijak náročný neni.
 Jeden způsob, jak si pomáhám s pamatováním čísel vizualizací, je vidět je jako ty stohy mincí nebo krabic nebo něčeho podobnýho. Pro každou číslici vidim jeden stoh. Nemám to jako kompletní metodu k zapamatování čísla, ale jako něco, co zkombinuju s dalšíma věcma. Taková pomůcka, kdyby něco selhalo.
Jeden způsob, jak si pomáhám s pamatováním čísel vizualizací, je vidět je jako ty stohy mincí nebo krabic nebo něčeho podobnýho. Pro každou číslici vidim jeden stoh. Nemám to jako kompletní metodu k zapamatování čísla, ale jako něco, co zkombinuju s dalšíma věcma. Taková pomůcka, kdyby něco selhalo.
Takže třeba pro číslo 6843 si to představíte jako 4 stohy krabic, viz obrázek.
Ve skutečnosti si spíš to číslo budete pamatovat nějak jinak, ale zároveň budete mít v hlavě jako pomůcku tu modrou šipku. U tý si nejspíš dokážete snadno vizuálně zapamatovat její tvar, tj. kdy jde dolu a kdy nahoru.
To znamená, že když třeba budete najisto vědět, který číslice tam byly, ale nebudete si jisti pořadím, ta šipka vám ho spolehlivě řekne. Víte, že první dvě čísla byly vyšší než ty druhý dvě, a víte, že ta hodnota postupně šla jednou nahoru a pak dvakrát dolu.
Nebo si kromě tý šipky zapamatujete, že první 3 číslice byly sudý a poslední lichá. To už vám dává hodně málo možností, jak to zvorat. Mohlo by to jinak bejt jedině 4621, ale to už zas nejste tak pitomí, abyste si spletli 6843 s 4621. Vždycky si aspoň něco z toho čísla zapamatujete přesně. Hlavně třeba čim to začíná. Kombinace několika pomůcek je taková pojistka.
Můžeme si zkusit zase nějaký delší náhodný číslo: 98632875
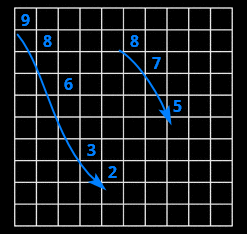
Nijak přehledný neni a na klávesnici nám to taky nic zajímavýho nedělá. Když si to ale představíme v tej mřížce, vidíme tu jistou posloupnost. Prvních pět čísel jde dolu, pak to skočí nahoru, a zbytek jde taky dolu. Zapamatujeme si, že začínáme od devítky a nejnižší je dvojka. Opakuje se nám jen osmička.
986 má stejnou posloupnost jako 875. Takže začínáme z horního rohu a jdeme o jedno dolu a pak o dvě – 986. Pak si třeba zapamatujeme tu třicet-dvojku normálně. A pak se nám opakuje ta první trojice, ale o pozici níž.
Samozřejmě mezi běžný pomůcky patří si to nějak rozdělit, jako 9863 2875, 986 328 75, nebo 9-863-2-875, podle toho, jak vám to dá něco, co je pro vás zapamatovatelný. Hodí se, když se v tom objeví nějakej letopočet nebo nějaký jiný známý číslo.
Konverze čísel na písmena
Další způsob, jak si pamatovat čísla, je zaměnit za ně písmena. Tahle metoda vyžaduje nějakej čas, protože se ji musíte “naučit”, ale jakmile ji ovládnete, je velmi efektivní. Spočívá v tom, že ke každej číslici přiřadíte nějaký písmeno (obvykle několik), a z delších čísel vzniknou slova, fráze, nebo věty, který se pamatujou líp než ty čísla. Ta věta se pak snadno konvertuje zpátky na to číslo.
Přidělení písmen k číslům si můžete vymyslet sami, jak chcete, nebo použít systém někoho jinýho, kterej najdete někde na Netu. Pointa je ke každej číslici přidělit nějakou souhlásku nebo několik. Samohlásky to bejt nemůžou, protože to by nefungovalo, jak si ukážeme za chvíli.
Asi nejběžnější používanej systém je popsanej tady, ale je dělanej pro angličtinu a v tejhle podobě pro češtinu asi nebude moc efektivní. Jde ale v podstatě jen o to, přidělit ke každej číslici tak dvě souhlásky, podle vlastního uvážení, a ten systém si zapamatovat.
Takže řekněme, že 1 bude L, 2 bude Z, a 3 bude M. Když si budete chtít zapamatovat číslo 213, dává to ZLM. Aby z toho vzniklo slovo, musíme si teď doplnit ty samohlásky – proto nemůžou bejt přidělený číslům. Ze ZLM teda uděláme slovo “ZLoM”. To si zapamatujete a až budete potřebovat to číslo, víte, že Z je 2, L je 1, M je 3 a samohlásky se nepočítaji.
Máte k dispozici zhruba 20 použitelnejch souhlásek na 10 číslic, takže to vychází dvě písmena na číslici. To vám pak dává víc možností. Kdyby číslo bylo 312 a nenapadalo vás žádný slovo na MLZ, pomůže vám, když dvojka bude kromě Z spojená třeba i s R, a varianta MLR už vám dá “MaLéR”.
Při konverzi zpátky to neni problém, protože jak Z, tak R vždycky odpovídá dvojce. Nicméně v češtině je celkem logický všude, kde to jde, přidat i varianty s čárkou nebo háčkem, takže MLZ může pak bejt “MLŽ”. Zároveň, když vás napadne, že slovo může samohláskou i začínat, tak se tu dá použít “eMuLZe” nebo “eMa LŽe”.
Můžete některý souhlásky nechat nepřidělený, a ty tak můžou hrát stejnou roli jako samohlásky. To může bejt užitečný v případech, kdy se z danejch písmen nedá nic kloudnýho vymyslet. Třeba když vás nebude nic napadat pro “KDST”, ale máte neutrální J, tak můžete použít “KDo jSTe”. Taky neni problém mít k nějakýmu číslu přiřazený jen jedno písmeno. Variant se dá vymyslet spousta.
Jiná varianta by byla použít ty písmena jako začátky slov a udělat z nich větu, takže KDST může bejt třeba “Kdo Dal Sýkorkám Televizi”.
Když máme na zapamatování 10-místný číslo, v písmenech z toho vyleze například PHRSMNVZHF. Výsledná fráze nemusí dávat žádnej smysl, takže tady z toho můžeme vydolovat “po hroším návozu haf”. To, že je fráze úplná kravina, je možná v podstatě dobře, protože o to líp si to zapamatujete. Taková blbost se vám nemůže s ničim splést. A člověk má prostě (většinou) od přírody mnohem lepší paměť na (i nesmyslný) fráze než na čísla.
Zároveň když většina číslic odpovídá dvěma souhláskám, tak PHRSMNVZHF je jen jedna varianta, jak to přeložit do písmen. Když jednomu číslu odpovídá P a B, tak na začátku tý fráze může bejt jedno nebo druhý. Bonus je i to, že se s tim nemusíte omezovat na češtinu, takže čím víc jazyků znáte, tím větší máte možnosti.
Trénování paměti obecně
Ačkoliv po vás ve škole chtěji, abyste si pamatovali až neskutečný množství letopočtů a jinejch hovadin, který vám nikdy k ničemu nebudou, už vás nenaučí jak si věci snadno pamatovat a jak paměť trénovat. Přitom na to taky existuje spousta metod. Co je tohle za vzdělávací systém?
Na jednu stranu se tu preferuje memorizace a opakování před samostatným myšlením a kreativní improvizací – což z lidí dělá nesamostatný autoritáře, a na druhou stranu tu neni žádná snaha o to, aby lidi měli dobrou paměť – což se zřejmě hodí, aby si lidi nepamatovali všechny ty sviňárny, co jim politici udělali před rokem. Výsledek tohodle “vzdělávacího” systému je, že se člověk naučí předvídatelně reagovat na povely a podněty, ale přitom nezíská žádný skutečný vědomosti a schopnosti.
Paměť se dá trénovat mnoha způsoby. Hlavní je tu paměť používat. Proto si málokdy píšu cokoliv, co se dá zapamatovat. Generace zvyklá mít všechny informace v mobilu a nepamatovat si vůbec nic je na tom dost špatně.
Zároveň ale existujou pomůcky, jak si pamatování ulehčit. To tu nebudu rozebírat moc detailně, protože koho to zajímá, může si na Netu vyhledat “jak si pamatovat věci” nebo tak něco. Popíšu jen jednu běžnou metodu, pro lepší představu.
Tenhle způsob se používá pro zapamatování si seznamu věcí, obvykle tak do deseti. Jako třeba co máte koupit v obchodě. Osobně jsem si nikdy nepsal seznam věcí na nákup, protože víc než 10 věcí nekupuju a psát si seznam kvůli 8 věcem je trapas, ale je na to snadná pomůcka.
Představte si nějakou svoji běžnou cestu, třeba z domova do práce. Na tej cestě si najděte 10 významnejch míst, úseků, atrakcí, nebo prostě cokoliv zajímavýho tam je. Tenhle seznam 10 zastávek na cestě budete používat, a má to tu výhodu, že to má i jasně daný pořadí.
Pro zkrácenej příklad řekněme, že máme na cestě autobusovou zastávku, kontejnery na tříděnej odpad, benzínu, a obchod se zmrzlinou. Pak dostanete za úkol jít nakoupit a přinýst chleba, klobásy, máslo a pivo. Abyste si zapamatovali, co máte koupit, spojíte si každou položku s jednim místem na tej cestě.
Takže chleba a zastávka – představte si, že na zastávku přijíždí velkej bochník chleba s oknama a nastupujou do něj lidi. Opět platí, že čim větší blbost, tim spíš to nezapomenete. A když je to něco zábavnýho, tak to je bonus. Klobásy a kontejnery – tady si třeba představíte, že ze všech těch kontejnerů lezou klobásy a hemží se všude okolo. Máslo a benzína – třeba tam někdo pomazal silnici máslem a všichni tankující po tom kloužou a padaji a rozlejvaji benzín kolem sebe. Pivo a obchod se zmrzlinou – můžete si představit, že vám někdo hodil zmrzlinu do piva, nebo nalil pivo do zmrzliny, nebo jak si zmrzlinář popíjí pivo, nebo jak chce za zmrzlinu místo peněz flašku piva… to je prostě jedno.
Jak si vytvoříte tyhle asociace, na zbytek dne si je v pohodě zapamatujete, i když jich bude 10 a klidně i víc. Můžete si ten systém vymyslet jak komplexní chcete. A podobnejch triků pro zapamatování si různejch věcí najdete víc, když vás to bude zajímat.
Jak je možný, že nás ve škole nenaučili ani jeden? Jak je možný, že takový věci člověk objevuje náhodně na Internetu, když je mu 30, 40, 50? Od čeho ta škola je?
Naučíte se hromadu letopočtů a bitev a válek (ze kterejch si ale evidentně celá společnost neni schopná vzít nějaký ponaučení), co kdo kdy napsal za knížku (aniž byste většinu z nich kdy četli), a papouškovat hromadu zbytečnejch faktoidů a lží, ale nenaučíte se myslet, nenaučíte se, jak si věci pamatovat, nenaučíte se řešit problémy, nenaučíte se žít. Prostě nic užitečnýho.
Pokud jde o trénování paměti, tak ji prostě v první řadě používejte, co to jde. Snažte se nedělat si zbytečně poznámky, když to neni moc náročný na zapamatování. Nakolik tu paměť používáte je otázka zvyku. Většina lidí je zvyklá ji nepoužívat a spolýhat místo toho na technologii. (Což asi nebude náhoda, protože to se vládnoucím parazitům náramně hodí.)
Jestli si někdy řikáte, “to určitě zapomenu”, tak s tim přestaňte, začněte si místo toho řikat “to si v pohodě zapamatuju” a prozkoumejte různý metody, jak to dělat efektivně. Hlavně to ale trénujte a zvykněte si spolýhat se na vlastní hlavu a ne na zápisníky, mobily, Internety, a podobně.
Každej Japonec se základním vzděláním se musí naučit hiraganu, katakanu a aspoň 2000 kanji! (Vysokoškolák si k tomu přidá dalších asi 2000 a dohromady jich je kolem 6000.) Divíte se potom, že jsou Japonci chytřejší než flákači z kolektivního Záchodu, co se ke čtení musí naučit jen asi 30 trapnejch písmen? A to ještě všichni Japonci umí i ty naše písmena a psát japonštinu těma.
Tady prostě nejsme zvyklí tu hlavu moc používat, ať už na myšlení nebo pamatování si.
Školství k hovnu
Náš “vzdělávací” systém je naprosto neefektivní, a když se objektivně podíváte na to, jaký jsou dneska možnosti versus co se ve škole opravdu učí, tak je nemožný si myslet, že je to nějaká náhoda nebo neschopnost. Je celkem evidentní, že tohle je záměr.
Ve světle ohromnejch změn v oblasti technologie, Internetu a přístupu k informacím za posledních 30 let by měly dnešní děti bejt 10x chytřejší než my, co už máme školu pár desítek let za sebou. Výsledek je ale úplně opačnej. Za náhodu to může považovat jen debil. Když výsledek perfektně odpovídá politickej agendě vládnoucí vrstvy, tak je zjevný, že je záměrnej.
Kdyby si dnešní děti místo roku ve škole přečetly pár hodnotnejch knížek, získaly by víc vzdělání za kratší dobu, bez vedlejšího efektu vymytýho mozku.
Školy tu jsou proto, aby vychovávaly poslušný otroky, a zajišťovaly, aby všichni věděli o stejnejch věcech a věřili stejnejm věcem, neměli žádnou samostatnost a ve všem byli závislí na autoritách, a neměli žádný opravdový znalosti, kterejma by mohli ohrozit ten parazitickej systém.
Kdo si myslí, že školy jsou tu pro vzdělání, je úplně mimo. Dobrá zpráva je, že se každej může vzdělávat sám, a s Internetem je to velmi snadný.
https://antivirus.22web.org/av/230910-vzdelavaci-system-na-nic-jak-se-neefektivne-uci.htm








