K nedávnýmu pojednání o zeměploše a zeměkouli, kterým se mi podařilo nasrat zase dalších pár lidí, si přidáme takovej menší bonus na tohle téma. Nedávno se objevil na Covid Logice článek Zvláštnosti nouzových přistání letadel. V něm nám autor prezentuje knihu s provokativním názvem “16 nouzových přistání, prokazujících plochou zemi”. Autor Covid Logiky k tomu za sebe píše:
Tento příspěvek slouží pouze k vyjádření pochybností, nikoli prezentaci jakéhokoli názoru a tímto autor prosí milé astronomy, geodety a vědce z oboru sférické geometrie, aby nás uklidnili a mohli jsme nadále klidně spát s vědomím, že nám ve škole opět nelhali 🙂
Než si astronomové a další vědci něco připraví, využiju toho, že se to víceméně sešlo s vydáním článku o tvaru Země na Antiviru, a navíc krátce po zveřejnění článku o argumentačních klamech. Celá tahle prezentace totiž používá několik argumentačních klamů, takže nám to sem hezky zapadne a ukážeme si, čím nás tu ti lívanci zase balamutí.
Pro pochopení, o co tu jde, si aspoň zběžně projděte ten článek. Víceméně se pointa dá pochopit z těch obrázků, ale ono tam toho textu stejně moc neni. Když to shrnu jednou větou, tak jde o to, že popsaný případy ukazujou nouzový přistání letadel v místech, který jsou na plochej Zemi přímo na trase letadla, zatímco na kulatej Zemi jsou – údajně – dost mimo trasu.
Je tady šikovně využitej argumentační klam “vybírání hodících se dat“. Bystřejší čtenář si všimne, že všechny popsaný případy jsou ze severní polokoule. Proč je to tak? Protože na jižní polokouli by tahle teorie totálně pohořela a nouzový přistání by na mapě plochý Země byly naprosto mimo.
Tohle by v podstatě jako vysvětlení mělo stačit, ale jelikož už to dneska moc lidem nemyslí a lívanci se plácaji v kognitivních zkresleních a argumentačních omylech, tak to rozeberu trochu víc do detailu, aby to bylo úplně jasný všem a lívanci z toho nemohli vybruslit nějakejma dalšíma pohádkama. (Oni to teda stejně udělaji a budou mě ignorovat, ale aspoň to snad pochopí většina lidí.)
V první řadě je dobrý si uvědomit, že pokud je Země kulatá, tak všechny “rovný” mapy jsou nutně zkreslený. Mapa ČR je zkreslená jen minimálně, protože ČR je v poměru k velikosti Země malá. Čím větší oblast chceme zmapovat, tím větší bude zkreslení. Největší zkreslení teda najdeme na mapách celýho světa.
Mapa má vždycky nějakej bod – obvykle střed – kde je zkreslená nejmíň, a se vzdáleností od toho bodu narůstá zkreslení. Na mapě světa je obvykle střed tam, kde se potkává rovník a nultej poledník.
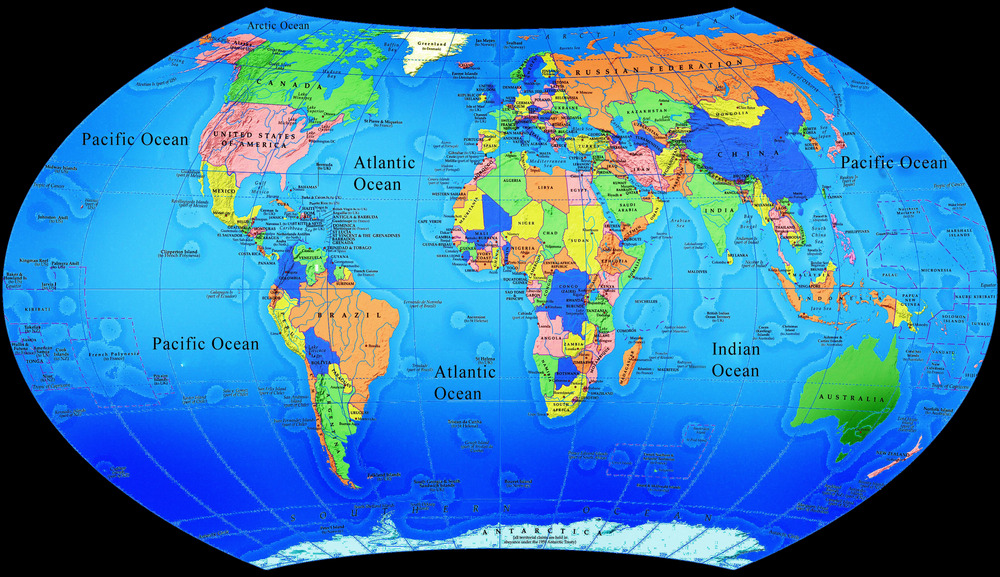
Tyhle dvě čáry teda vidíme jako rovný, zatímco ostatní poledníky a rovnoběžky jsou zakřivený, protože se ve dvourozměrnym prostoru pokoušíme zobrazit trojrozměrnej objekt. Tahle mapa světa je nejpřesnější tam, kde se protíná rovník a nultej poledník, tj. v Guinejskym zálivu. Od tohodle bodu se pak na všechny strany mapa víc a víc zkresluje.
Mapa se dá nakreslit různejma způsobama a mapy světa nejsou všechny stejný. Autor mapy si musí vybrat, jak na to chce jít a kterou část mapy chce mít nejpřesnější a kde je naopak ochotnej přesnost obětovat. Tady se můžeme podívat na dva příklady různejch zobrazení.
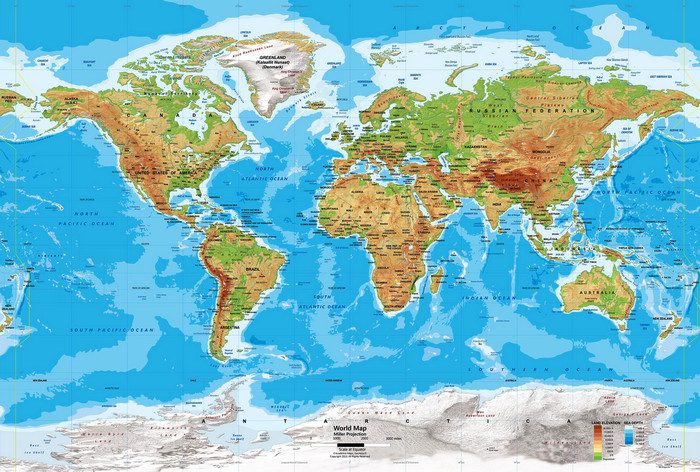
Obě mapy maji rovnoběžky i poledníky rovný, ale mapa nahoře má ohromně zvětšený části kolem pólů, zatímco mapa dole regiony směrem na sever a jih postupně zmenšuje. Tahle druhá reprezentace dává lepší představu o poměru velikostí kontinentů – na rozdíl od mapy nahoře je tu správně vidět, že Afrika je větší než Severní Amerika. Nicméně rovníková část je natažená do vejšky a sever a jih do šířky.
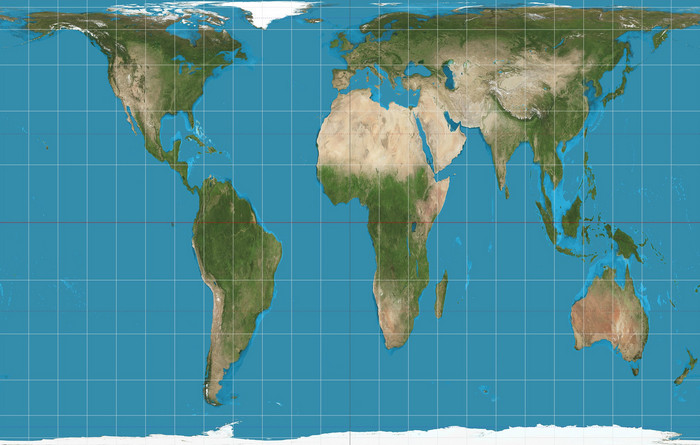
Jakákoliv mapa kulatý Země má teda nějaký zkreslení, který je do jistý míry arbitrární – podle toho, jakou metodu si autor mapy vybere.
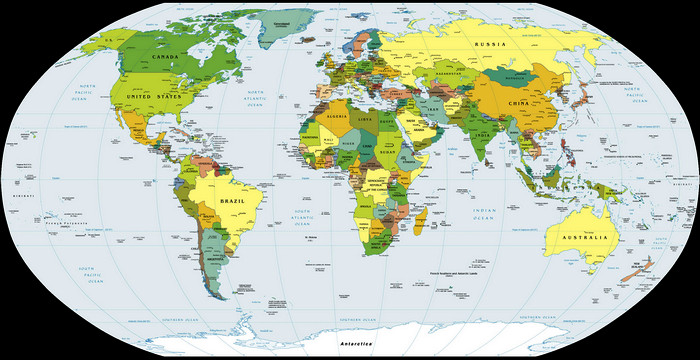
Když se podíváme na tuhle běžnou verzi mapy Země, tak podél rovníku je zkreslení minimální, díky tomu, že je použitej jako základ tý mapy. Je prostě navržená tak, aby rovník byl ta nejpřesnější část. Další relativně přesná část je ten nultej poledník (v tomhle případě kousek na východ od něj), ale směrem na sever a jih zkreslení narůstá víc než na východ a západ.
Nejvíc zkreslení narůstá diagonálně od středu, takže nejmíň přesný části mapy jsou její rohy. Tohle všechno byste měli vědět ze základní školy, protože nás to tam učili (no, aspoň ty starší ročníky), ale jelikož mnozí evidentně většinu svýho základoškolskýho vzdělání zapomněli, tak to radši vysvětluju.
Proč je zkreslení mapy důležitý? Protože v něm je celej tenhle trik lívancovýho argumentu. Mapa plochý Země má střed na severním pólu.
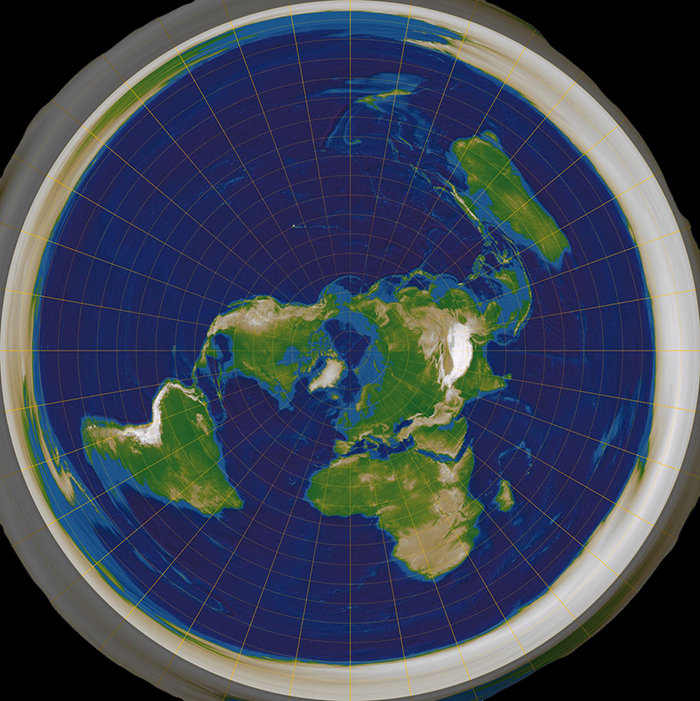
Tahle mapa zároveň reprezentuje i kulatou Zemi – pořád z toho vyčteme, kde co je – ale s tím, že tady máme nejmenší zkreslení na severním pólu a největší na jižním. Jižní pól je jeden bod, stejně jako severní, ale tady je roztaženej po obvodu celý mapy, což je v podstatě úplně maximální zkreslení.
Jak hodně se na mapě světa můžou věci zkreslit, můžete vidět třeba na příkladu Grónska, který leží v tej obvykle hodně zkreslenej části.

Tady například vidíte Grónsko třikrát větší než Austrálii, což je samozřejmě naprostá kravina. Austrálie je ve skutečnosti tři a půl krát větší než Grónsko. Stejně tak Afrika, jak už bylo řečeno, je podstatně větší než Severní Amerika, ačkoliv to tak na mnoha mapách nevypadá.
Co z toho všeho vyplývá? Vyplývá z toho, že pokud chcete něco vidět na mapě realisticky, obzvlášť když jde o velký vzdálenosti (jako ty mezinárodní lety), neměli byste čumět na 2D mapu, ale na glóbus! Tam je zkreslení naprosto minimální. (Nějaký tam teoreticky je třeba proto, že rovník je o něco delší než poledníky, ale to je zanedbatelnej rozdíl.)
Když si najdete samostatnou mapu Grónska, bude vypadat o dost jinak, než na mapě světa. Střed mapy totiž nebude v Guinejskym zálivu, ale přímo v Grónsku. Čehokoliv chceme mít mapu, navrhneme ji tak, aby byl střed projekce na místě, který chceme vidět nejpřesnějc.
No a mapa plochý Země má střed na severním pólu, a tudíž oblast kolem severního pólu je na tejhle mapě nejpřesnější i pro kulatou Zemi. Nicméně zároveň s tim je mapa plochý Země nejmíň přesná na jižním pólu. Zatímco na zeměkouli maji oba polární kruhy stejnou dýlku, kolem 16 tisíc km, na plochej Zemi má severní polární kruh obvod asi 16300 km, zatímco ten jižní má asi 109300 km, takže je 6.7-krát delší.
Když se podíváte na obrázky v tom článku, vidíte tam mapu plochý Země (což je v podstatě to samý jako mapa kulatý Země se středem na severním pólu a největším zkreslením na jižním) a obvyklou mapu světa, a k tomu rovnou čáru pro trasu letadla.
To už je ale klam, protože na kulatej Zemi tahle rovná čára v žádnym případě nereprezentuje nejkratší cestu z bodu A do bodu B, a tudíž tudy to letadlo rozhodně nepoletí. Pro lepší představu, kudy to letadlo asi tak poletí, se musíte podívat na glóbus a najít si nejkratší cestu na něm.
Zjistíte tak, že nejkratší trasa nikdy neni taková, jako na normální rovnej mapě, ale na severní polokouli se bude vždycky vychylovat směrem na sever, a na jižní naopak. Takže jeden klam – nepochybně záměrnej – tu spočívá v tom, že se ukazujou rovný čáry na zkreslenej mapě, a čtenářům se podsunuje naprosto mylnej dojem, že to by na kulatej Zemi měla bejt trasa letadla. (Je to příklad argumentu straw man.)
Jelikož všechny lety použitý k argumentaci pro plochou Zemi jsou z bodu A na severní polokouli do bodu B na severní polokouli, střed trasy se nutně bude vychylovat k severnímu pólu. Ty nejdelší trasy, kde jsou body A a B na opačnej straně Země, a tudíž ve směru východ-západ tak daleko od sebe, jak jen to jde (180°), povedou přímou čarou přesně přes severní pól.
Příkladem je případ letu San Francisco – Dubaj. Autor knihy nakreslil mezi oběma městy rovnou čáru na plochej mapě, ačkoliv když si vezmete glóbus, zjistíte, že na kulatej Zemi přímá trasa vede přes severní pól. Mezipřistání v Moskvě potom neni ani trochu zvláštní.
Mimochodem, pokud nemáte k dispozici glóbus, použijte měření vzdálenosti na google mapách (aspoň pro jednou budou ti šmejdi k něčemu užiteční). Google totiž bere v úvahu tvar Země a tu trasu mezi dvěma body vám nakreslí ne rovně, ale tudy, kudy je nejkratší na kulatej Zemi nebo na glóbusu.
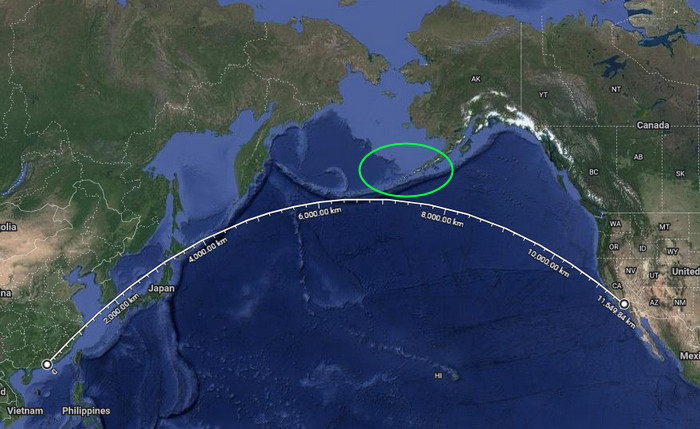
Tady je skutečná nejkratší trasa z Hong Kongu do Los Angeles na kulatej Zemi. Autor knihy bere to, že nouzový přistání bylo na Aleutskejch ostrovech (zelenej ovál), jako důkaz toho, že Země je plochá. Ve skutečnosti je jeho argument důkazem toho, že je to buď nevzdělanej debil, nebo lhář a podvodník, protože ty ostrovy jsou prakticky přesně na trase HK-LA. A kromě toho tu ani neni žádný jiný místo, kde by se dalo přistát.
Jelikož mapa “plochý Země” je ve skutečnosti prostě jen mapa s nejmenším zkreslením kolem severního pólu, je logický, že pro dlouhý lety na severní polokouli je to poměrně ideální 2D zobrazení, a že bude pro takový případy přesnější než standardní mapa světa, která je zaměřená na rovník a směrem k pólům extrémně zkreslená.
Ohledně toho je ale třeba vést v patrnosti dvě věci. Za prvý, mapa plochý Země by se tu neměla srovnávat s “mapou světa”, ale s glóbusem, a za druhý, mapa plochý Země bude na jižní polokouli o to zkreslenější, o co se zdá přesnější na tej severní. Takže proč si asi tak myslíte, že všechny ty příklady v knize jsou ze severní polokoule? (Jeden příklad z jihu tam ve skutečnosti je, ale ten jen dává za pravdu kouli – k tomu se dostaneme.)
Můžeme si názorně ukázat, jak by to fungovalo na jižní polokouli. Řekněme, že bysme chtěli letět ze Sydney do Rio de Janeiro. Lívanec by nám nakukal, že by trasa měla vypadat takhle.
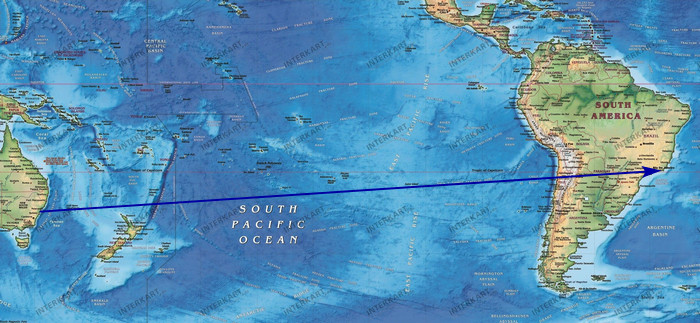
To je samozřejmě kravina. Skutečná nejkratší trasa vychází nějak takhle:

Na glóbusu to vypadá zhruba nějak takhle:
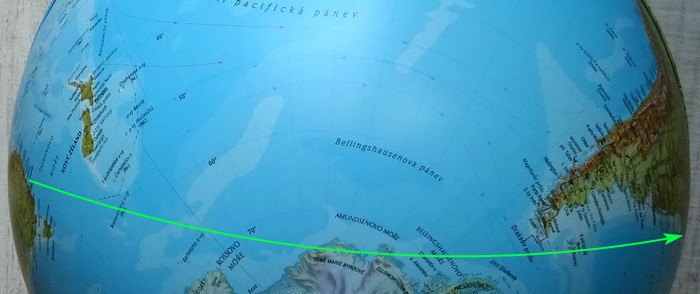
Letělo by se přes Antarktidu, a nouzový přistání by logicky mohlo bejt někde na jihu Argentiny, nebo na Falklandách, což by na prvním obrázku vypadalo zvláštně. Legrace je, když se na tuhle trasu podíváme na mapě plochý Země:
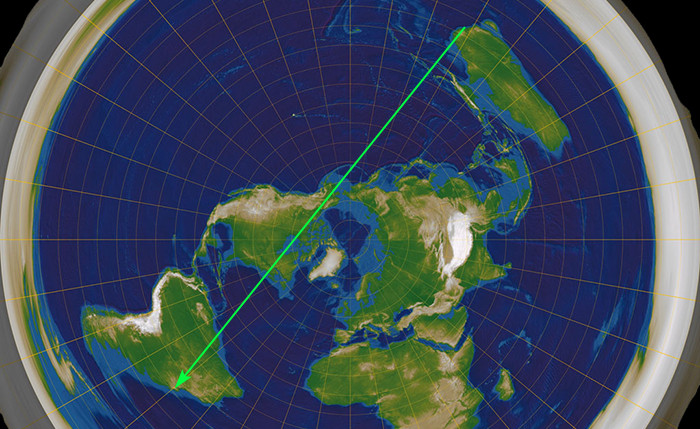
Lívanci si myslí, že by ze Sydney do Ria letěli přes Kanadu a v podstatě kousek od severního pólu, ačkoliv skutečná trasa vede přes Antarktidu.
Ještě je třeba poznamenat, že nejkratší cesta neni nutně ta, kterou letadlo poletí. Letadla využívaji vzdušnejch proudů, který dokážou let značně zrychlit. Například let z L.A. do N.Y trvá kolem 4 hodin a 45 minut, zatímco opačným směrem trvá kolem 5 hodin a 20 minut, protože vzduch tu proudí na východ.
Tohle je významnej faktor, a ty proudy jsou na různejch místech různý. To znamená, že když může letadlo nějakýho toho výhodnýho proudu využít, tak si klidně 100-200 km zaletí, aby ten proud chytlo, protože se to vyplatí, a naopak, když je trasa proti takovýmu proudu, tak je dobrý let odklonit někam, kde takovej protivítr neni. Má to vliv nejen na dobu letu, ale taky na spotřebu paliva. Zatímco aerolinkám je u prdele, jestli někam přiletíte pozdě, rozhodně jim neni u prdele, kolik je to bude stát.
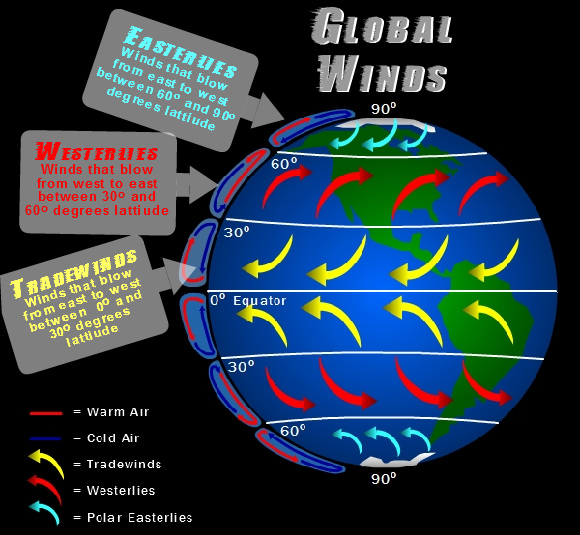
Samozřejmě druhá věc je počasí. Když to neni nutný, letadla nelítaji přímo do středu bouřky, takže podle toho, kde je nějaká ta bouřka (kterejch může bejt na dlouhej trase hodně), se může skutečná trasa různě odchylovat od tý nejkratší možný.
I když se teda podíváme na nejkratší trasu, zdaleka to neznamená, že tudy se opravdu letí. Vzdušný proudy a počasí můžou lety všelijak odklonit. Takže i v případech, kdy to vypadá, že nouzový přistání je přece jenom zbytečně mimo trasu, musíme brát v úvahu, že víme prd, kudy se přesně letělo a proč.
A třetí faktor je, že to samozřejmě nefunguje tak, že si pilot může přistát, kde chce. To letiště pro něj musí mít místo a obecně vhodný podmínky, včetně toho počasí. Pokud nejbližší letiště má zrovna hodně dalších letů a už tam nemůže nic vtěsnat, musí pilot hledat jinde. To jen lívanci si myslí, že svět funguje tak jednoduše, jak si to představujou ve svejch hlavách, a že se vždycky všechno děje podle jejich předpokladů. Běžně se může stát, že letadlo poletí trochu dál na nějaký větší letiště, protože to bližší a menší to zrovna nezvládá.
A reálnej svět je samozřejmě ještě komplikovanější. Taky záleží na tom, z jakýho důvodu přesně to letadlo potřebuje přistát, a jestli to nejbližší letiště má prostředky na to, aby ten problém vyřešilo. Kromě toho, protože lidi jsou debilové, tak se musí brát v úvahu i politika, a v současnej době třeba ruský letadlo může mít problém přistát na spoustě zfanatizovanejch míst v kolektivním Záchodě, stejně jako americký letadlo asi nebude chtít přistávat v Rusku.
Jenže jak vidíme tady v tej knize, lívanec si prostě nakreslí rovnou čáru, nechápe ani zlomek relevantních faktorů, a když se věci nedějou podle jeho přitroublejch, infantilních představ, vyvozuje z toho idiotský závěry a ještě je pak cpe ostatním jako “důkaz”.
Takže si projdeme pár příkladů z tý knihy a ukážeme si, jak je to doopravdy na kulatej Zemi, o čemž autor knihy buď nemá ani páru, nebo záměrně klame. (Těžko říct, která varianta je horší.) Let H.K.-L.A. s přistáním na Aljašce už jsme viděli. Máme tu podobnej let – Taipei-L.A. – s přistáním v San Franciscu. Autor se pozastavuje nad tim, proč by letadlo letělo do S.F., vzdálenýho 380 mil od L.A..
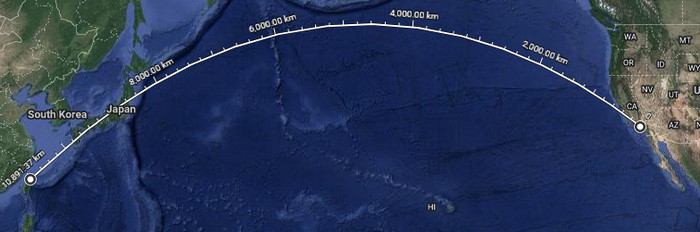
Skutečná trasa ale vypadá takhle. Kde je San Francisco?
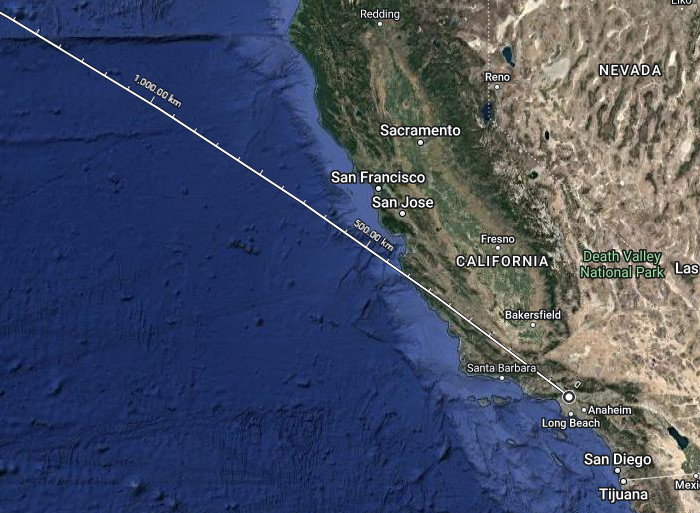
Jen asi 100 km mimo trasu, což je na 11 000 km dlouhej trase jako nic. Když se na tu trasu podíváte, je přistání v S.F. naprosto logický. Autor vám ale namaluje, kudy by trasa “měla jít”, udělá to naprosto špatně, protože je debil, a když se realita nepřizpůsobí jeho omylu, bere to jako důkaz plochý Země.
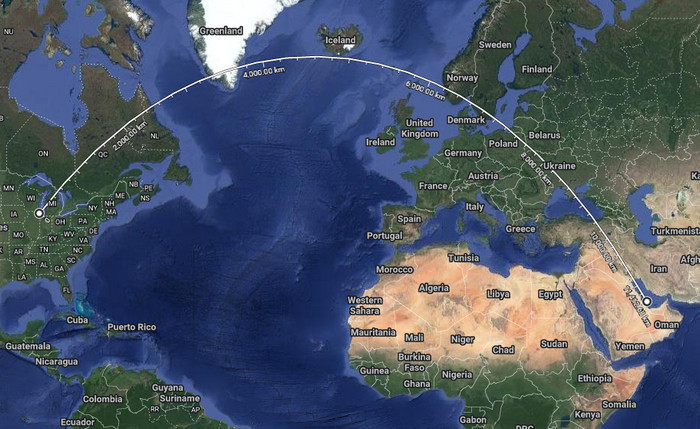
Tady máme let Chicago-Doha, u kterýho lívance překvapuje, že se přistálo v Moskvě. Předpokládanou cestu si totiž nakreslil přes Afriku.

Jak vidíme, Moskva neni nijak daleko mimo trasu. A jak jsem vysvětlil, kvůli proudům vzduchu, počasí, atd., se ve skutečnosti mohlo letět trochu jinudy. Moskevský letiště bude taky v okolí pravděpodobně největší a nejlíp vybavený. Každopádně by byla absolutní blbost přistávat v Africe.
Ještě markantnější je to u letu San Francisco – Dubaj. To je jeden z nejdelších letů a je to ten případ, kdy jsou města na opačnej straně zeměkoule. S.F. je 122° západně a Dubaj je 55° východně. To je rozdíl 177°, tedy téměř 180, což znamená, že přímá cesta vede skoro přesně přes severní pól.
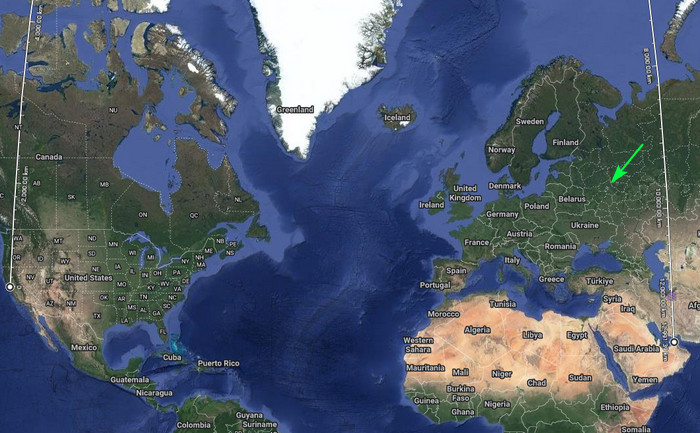
To vidíte na tom, že tady ta nejkratší cesta vede z obou míst prakticky kolmo nahoru. V tomhle případě je trasa na kulatej Zemi vlastně úplně stejná, jako na plochej Zemi. Moskvu, kde se přistálo, ukazuje zelená šipka. Jakákoliv jiná možnost je prakticky na Sibiři, takže se neni co divit, že to vyšlo na Moskvu.
Kromě toho, skutečná trasa na kulatej Zemi je od Moskvy úplně na druhou stranu, než ji autor knihy předpokládá. Napadá mě, že lívanci možná nějak postrádaji prostorovou představivost a cokoliv trojrozměrnýho je na ně moc složitý a nedokážou si to ani představit, natož to pochopit, takže pro ně všechno musí bejt plochý a dvojrozměrný, aby jim to dávalo smysl. (Je to jen takovej blbej nápad, ale mám pocit, že by to leccos vysvětlovalo.)
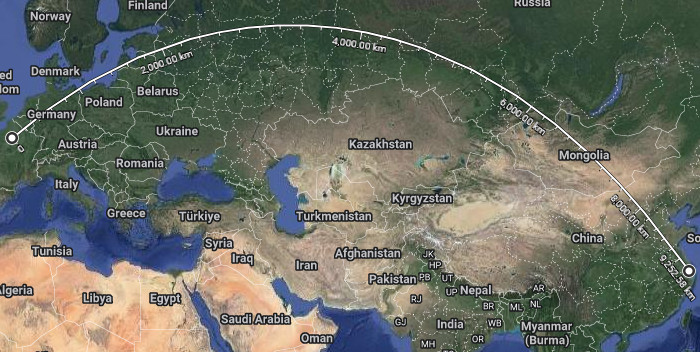
Tady máme let Paříž-Šanghaj. Nouzový přistání v Irkutsku. Problém?
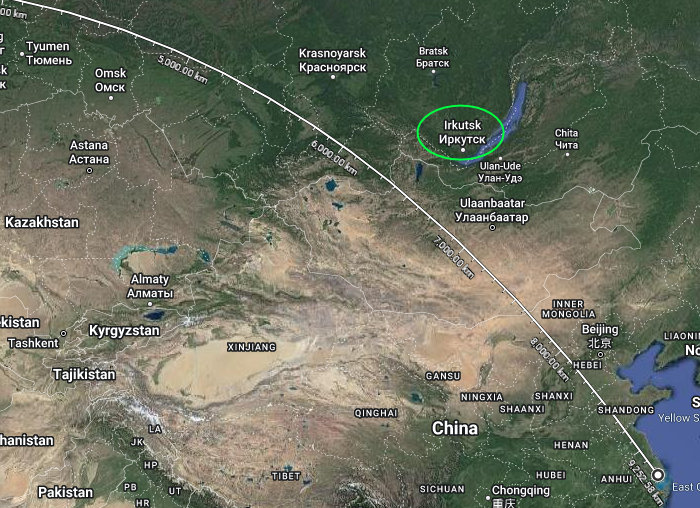
Let z Dallasu do Pekingu:
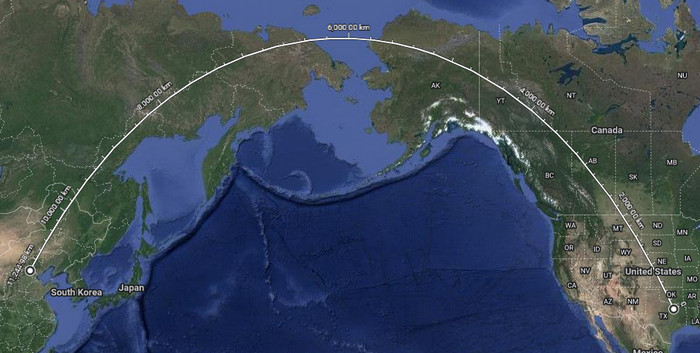
Letadlo přistálo v Calgary.
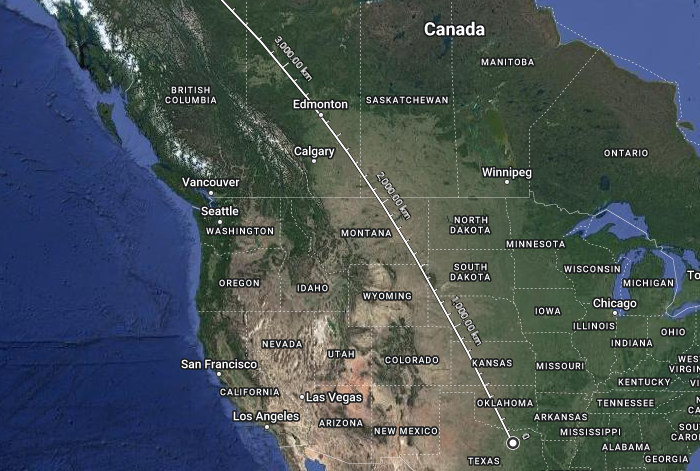
Což je asi 100 km od trasy. Fakt překvapivý. Lívanec ale čekal, že se poletí přes L.A.
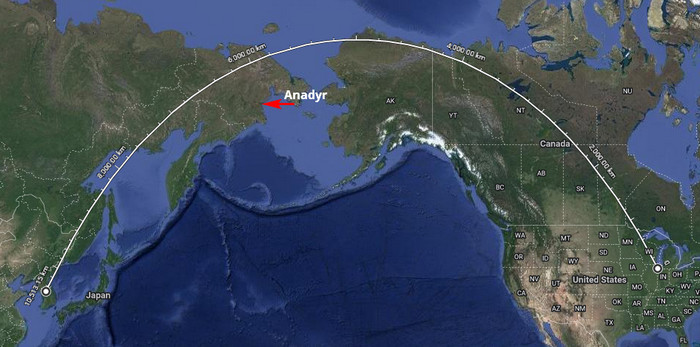
Let ze Soulu do Chicaga s přistáním v Anadyru na Čukotce. Opět záhada jak prase. A opět je trasa ve skutečnosti ještě na sever od Anadyru, a ne na jih, jak si myslí lívanec.
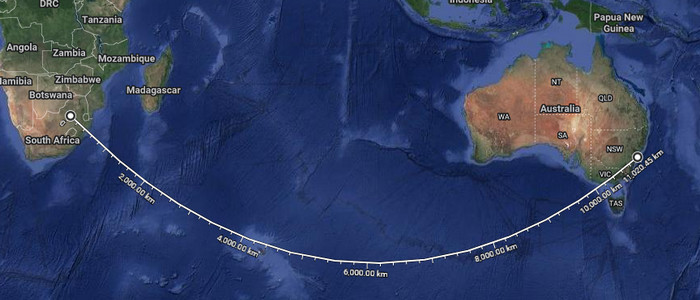
Poslední příklad – let z Johannesburgu do Sydney. Tady máme ten jeden příklad na jižní polokouli. Proč tady je? Protože po lívancovi specificky někdo chtěl, aby ho vysvětlil. Lívanec tady přiznává, že letadlo ve skutečnosti přistálo tam, kde to dává na kulatej Zemi smysl. On si samozřejmě tu čáru nakreslil rovně, takže to vyšlo úplně přesně, ale ve skutečnosti jde trasa mimo.
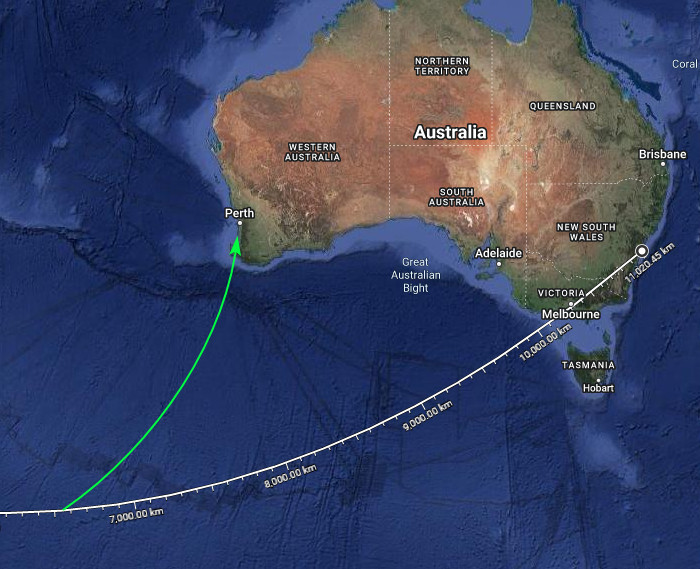
Jenže kde jinde by se tu asi dalo přistát? Leda v Antarktidě a to by asi nebyl dobrej nápad, i kdyby tam někde bylo letiště.
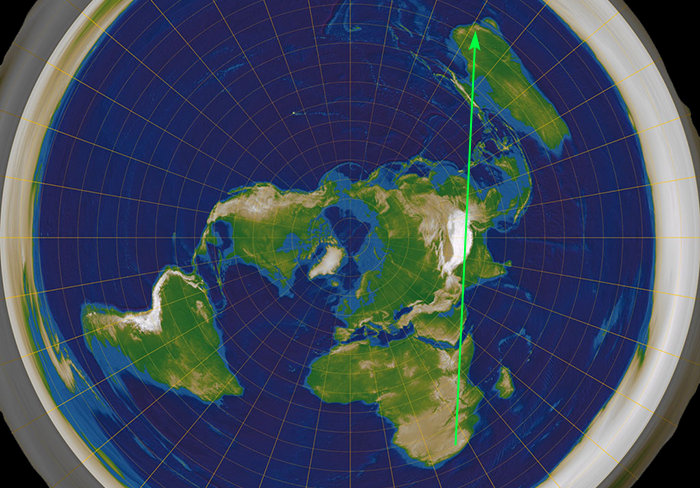
Na plochej Zemi ta trasa ale vede přes Etiopii, Pakistán, Čínu a Filipíny. Neboli přesně jak jsem říkal, na jižní polokouli to lívancům ani trochu nevyjde. Autor knihy to pak musí vysvětlovat těma vzdušnejma proudama (způsobenejma točením kulatý Země!) – který zohledňuje jen tady, kde mu to nevyšlo, jak potřeboval. Nicméně že by si letadlo kvůli vzdušnejm proudům zaletělo 6000 km mi připadá jako docela hodně.
Glóbus
Jelikož jsem čekal, že kognitivně zkreslení a argumentačně klamaví lívanci by mohli začít hejkat, že Google tam ty čáry kreslí špatně a je to všechno konspirace a podvod, půjčil jsem si ten glóbus, vzal si provázek a pár těch tras tam vyznačil a vyfotil. Šipky ukazujou, kde přesně jsou místa startu a cíle a kde byly nouzový přistání. Obrázky si můžete zvětšit, aby se to dalo líp přečíst.
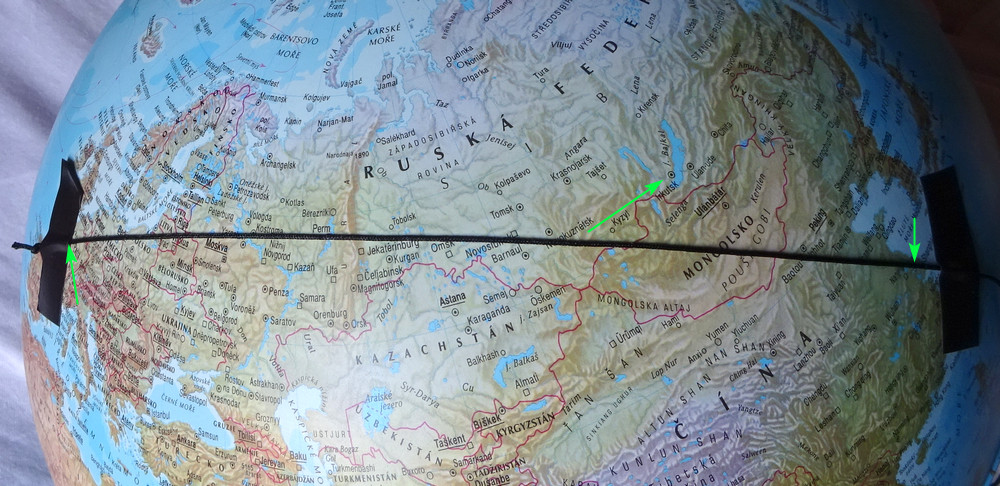
Paříž-Šanghai, zastávka Irkutsk.
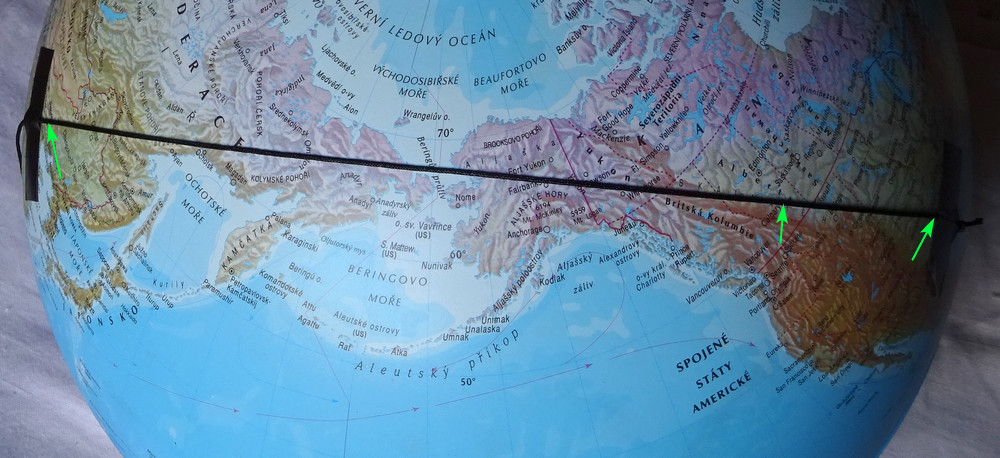
Dallas-Peking, zastávka Calgary. Naprosto přesně na trase.

Soul-Chicago, zastávka Anadyr.
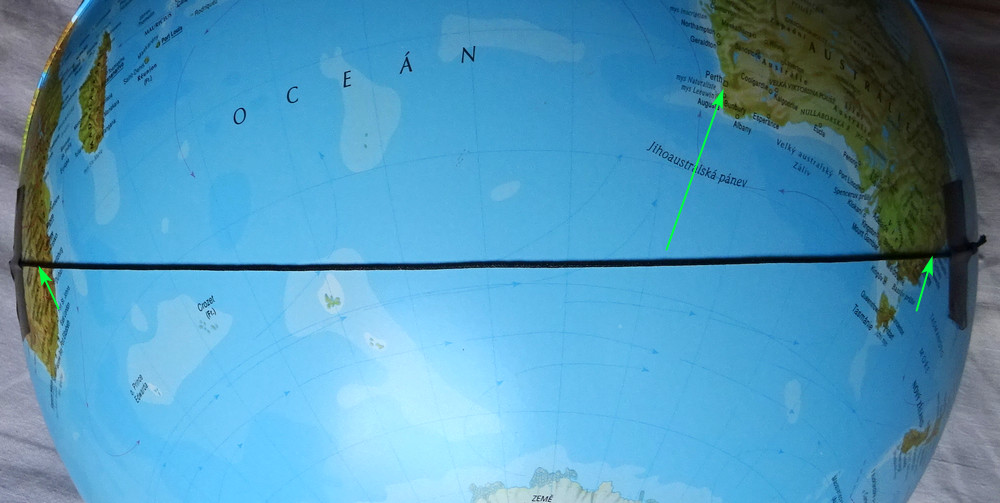
Johannesburg-Sydney, zastávka Perth.
Nakolik můžu posoudit, Google ty křivky má trochu víc vychýlený k pólům, než mi to vycházelo na glóbusu. Abych měl měření co nejpřesnější, držel jsem provázek na obou koncích, našponoval ho a posunoval sem a tam ve směru “letu”, aby se usadil na tej nejkratší trase, takže si nemyslim, že tam mám výrazný odchylky.
Uvažoval jsem, jestli to může bejt tim, že rovník je delší než poledníky, ale to je rozdíl jen 0.3%, takže to asi ne. Předpokládám teda, že Google ten algoritmus nemá úplně přesně vyladěnej. Ale rozdíly od mýho měření jsou tak o 2%, takže to neni nic závažnýho.
Pokud nevěříte ani Googlu, ani mně, máte to štěstí, že si snadno můžete sehnat glóbus a všechno si to ověřit sami.
Lety
Pro zajímavost a lepší představu se můžeme podívat, jak vypadaji trasy letů z různejch měst.
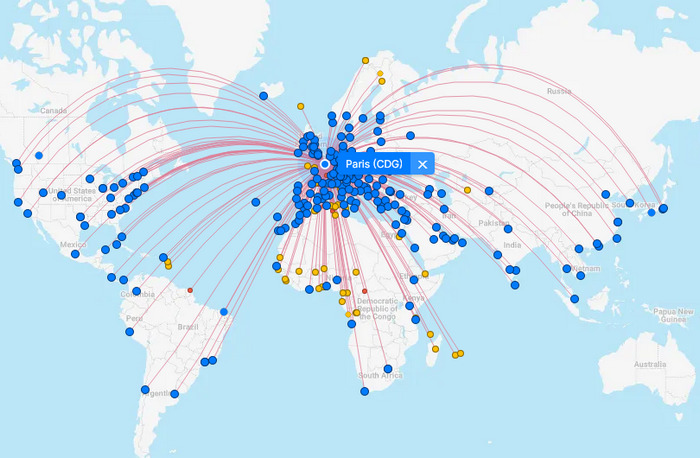
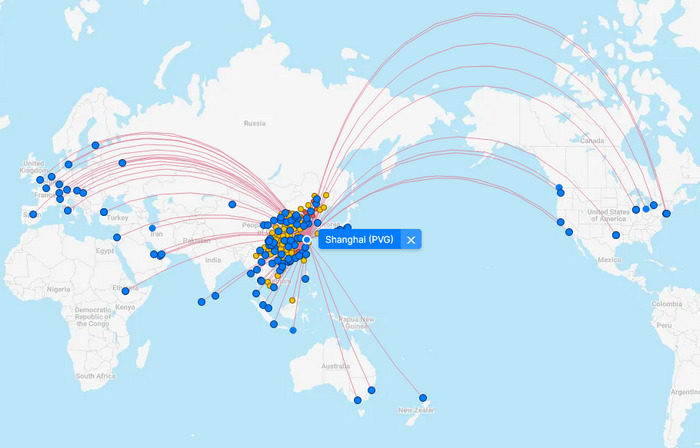
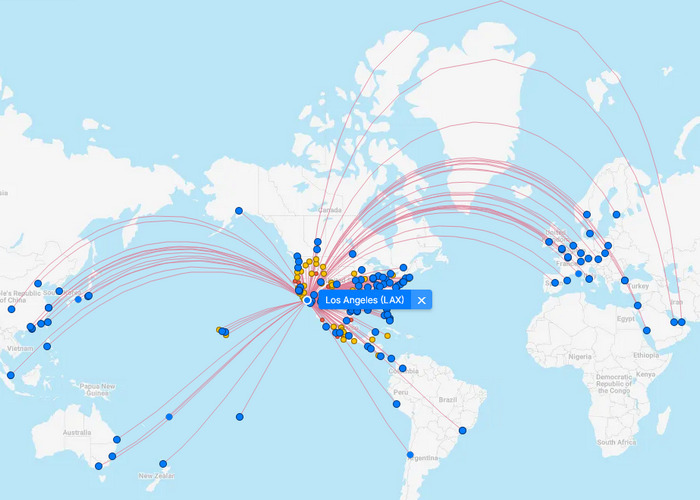
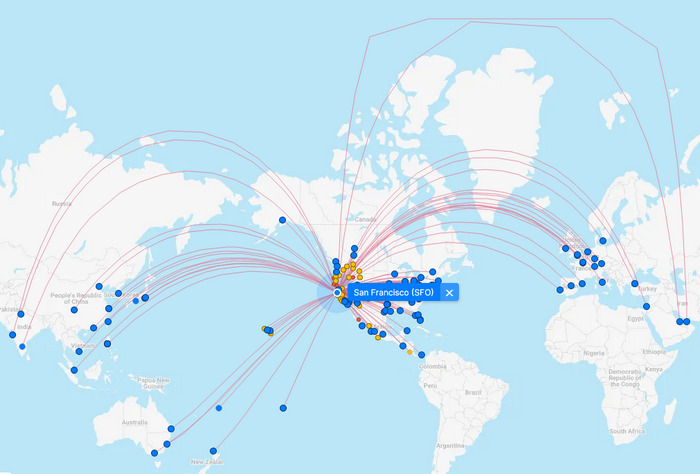
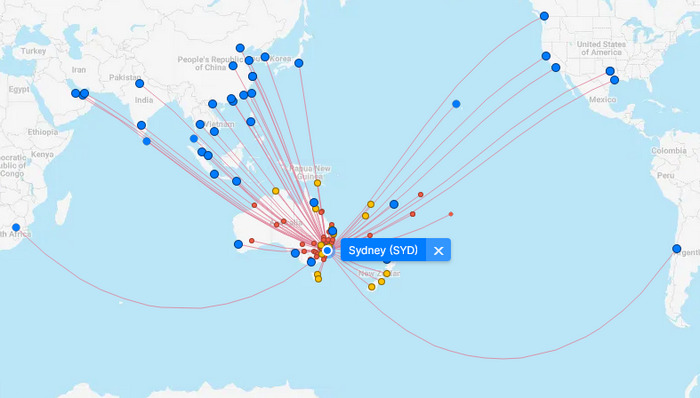
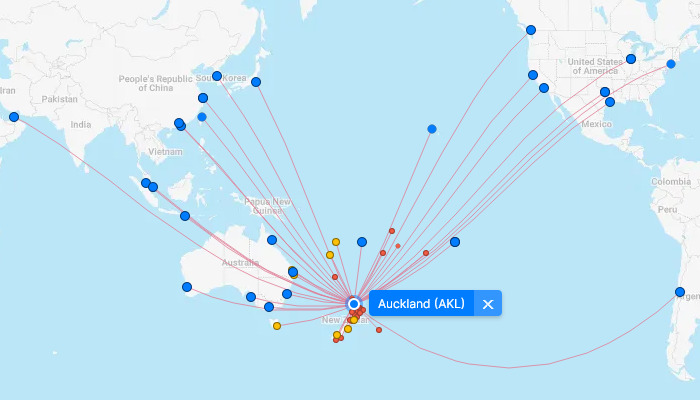
Vidíte, že čím jsou ty trasy na jednej polokouli delší, tím větší jsou ty oblouky. To vypovídá o zkreslení tý mapy, protože na glóbusu jsou ty trasy všechny přímý. Kdo by si tyhle mapky letů chtěl otestovat sám, může jít na www.flightconnections.com a vyzkoušet si různý trasy.
Zároveň vám to řekne, jak dlouho kterej let trvá, což je další ukázka něčeho, co rozdrtí teorii plochý Země na prach. Můžete si to vyzkoušet sami, takže tady dám pro ilustraci je jeden příklad severního letu a jeden jižního.
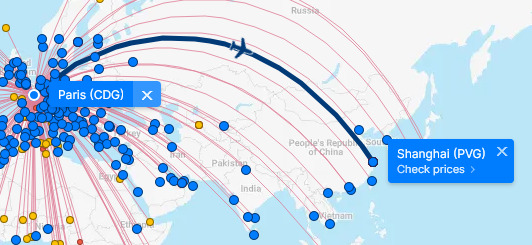
Let Paříž-Šanghaj trvá 12 hodin a 25 minut. Opačným směrem je to 14 hodin. (Vzdušný proudy.)
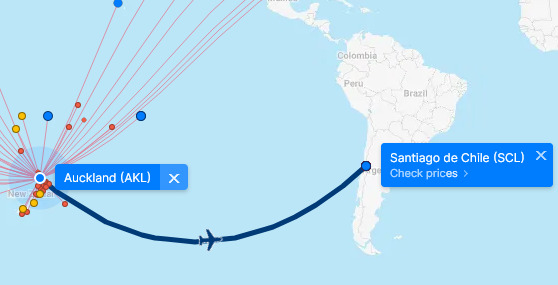
Auckland-Santiago trvá 11 hodin a zpátky 12 hodin a 45 minut. Obě trasy jsou podobně dlouhý (asi 4% rozdíl). Mapky tu máte ve stejnym měřítku a můžete si to vyzkoušet na těch stránkách nebo na glóbusu, takže vidíte, že ty trasy vypadaji podobně. Jak to vypadá na zeměploše?
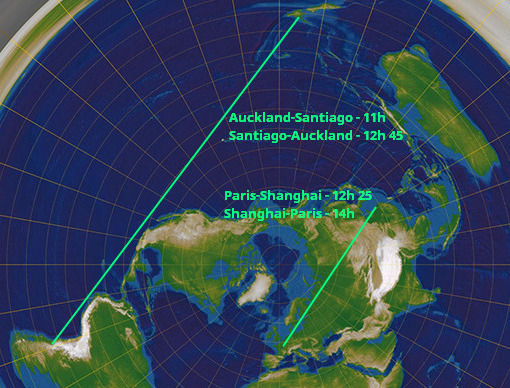
Trasa Auckland-Santiago je na plochej Zemi 2.44x delší než Paříž-Šanghaj. Jak je možný, že ji letadlo zvládne rychlejc?! O tom lívance mluvit neuslyšíte.
Závěr
Lívanec si ze všeho vyvodil, že Země je plochá, protože nouzový přistání neodpovídaji tomu, jak to podle něj má vypadat na kulatej Zemi. Jelikož si ale evidentně nedokáže představit, jak ta kulatá Země vůbec vypadá, všechny jeho předpoklady byly mylný a stupidní a pak mu to samozřejmě nevyšlo.
Tragický na tom je, že jak jste právě viděli, stačí si vzít glóbus a provázek a během pěti minut víte, že to všechno na kulatej Zemi dokonale odpovídá a dává smysl. Že je někdo tak blbej, že tohle neni schopnej udělat a na bázi svojí mylný představy napíše celou knížku, je na pováženou. Těžko říct, jestli je horší bejt zombík nebo takovejdle lívanec, protože zombíky jejich hloupost aspoň nestojí žádnou energii.
Viděli jsme, že všechno, co lívancovi nahrávalo k jeho teorii, bylo na severní polokouli, a vysvětlili jsme si, proč to na severní polokouli bude jeho mapě celkem dobře odpovídat. K tomu jsem vysvětlil, proč by to lívancům na jižní polokouli nikdy nevyšlo, což se tím jedním případem, kdy tam ta jižní polokoule byla, potvrdilo. Hlavně jsme si ale na všech příkladech ukázali, že na glóbusu nám to všechno vyjde úplně bez problémů.
Nelze než poznamenat, že lívanci by měli přestat vytahovat neexistující problémy a měli by si radši prohlídnout glóbus a pokusit se pochopit, jak taková koule vůbec vypadá, protože tohle vážně žádný vyšší vzdělání nevyžaduje.
https://antivirus.22web.org/av/230413-nouzovy-pristani-letadel-a-tvar-zeme.htm?i=1