Jelikož se v posledních letech šíří názor, že Země je plochá a ne kulatá, prozkoumal jsem argumenty pro tuhle teorii, jestli na ní něco je. Ukázalo se jasně, že neni. Napsal jsem o tom dva články:
1. Žijete na zeměploše nebo na zeměkouli? / 2. Nouzový přistání letadel a tvar Země
V prvním jsem tak nějak obecně rozebral teorii plochý Země (PZ) a poukázal na její největší problémy. Prezentoval jsem 16 otázek, na který bych chtěl od zastánců PZ odpovědi, pokud bych měl tu teorii brát vážně. Sklidil jsem od nich spoustu kritiky a urážek, ale nikdo neodpověděl ani na jednu otázku.
Druhej článek byl reakcí na knihu, která tvrdí, že místa nouzovejch přistání letadel dokazujou, že Země je plochá. Jasně jsem tam ukázal, že všechny ty přistání nic takovýho nedokazujou, protože jsou naprosto konzistentní se zeměkoulí. Autor knihy je buď nějakej agent, nebo blb, kterej neví, jak vypadá koule.
Tady hlavně vysvětlim, proč víme (ne “myslíme si”), že je Země kulatá. Jelikož spousta věcí byla detailně vysvětlená už v těch článcích, nebudu všechno opakovat a budu na ně odkazovat jako na “PZ1” a “PZ2”. Jak bylo zavedeno v PZ1, pro zjednodušení říkám lidem z kulatý Země melouni a z plochý lívanci.
Model plochý Země říká, že Země je placka, která vypadá zhruba takhle:
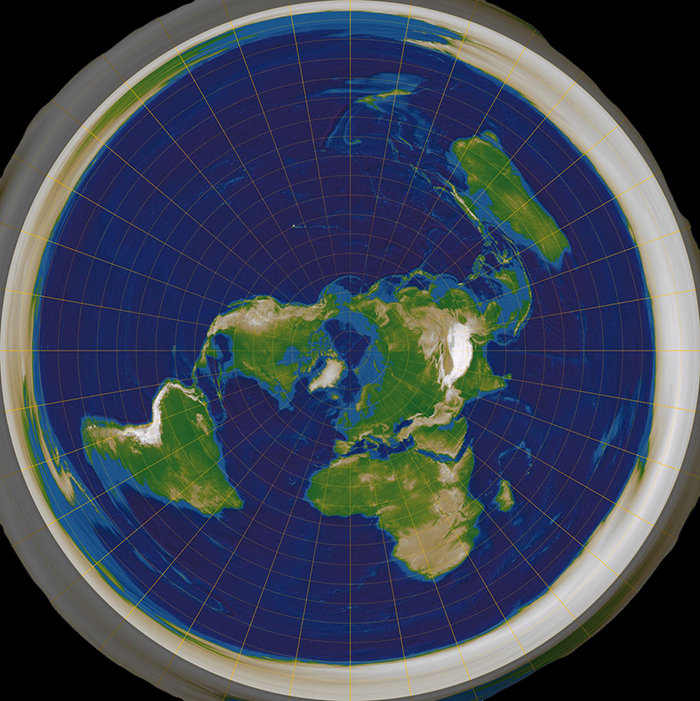 Součástí modelu je, že slunce a měsíc jsou koule asi 51 km v průměru, který se pohybujou několik tisíc kilometrů nad zemí. Dokázat skutečnej tvar Země neni nijak těžký, a to, že slunce je od nás hodně daleko, už vůbec ne.
Součástí modelu je, že slunce a měsíc jsou koule asi 51 km v průměru, který se pohybujou několik tisíc kilometrů nad zemí. Dokázat skutečnej tvar Země neni nijak těžký, a to, že slunce je od nás hodně daleko, už vůbec ne.
Tenhle přehled rozdělim do tří částí: důkazy pro kulatost Země, odpovědi na častý otázky lívanců, a nesmyslný tvrzení a lži lívanců. Nakonec si řekneme něco o tom, jak lívanci operujou a proč se asi tohle všechno děje. Účelem tohodle pojednání je ukázat lidem, kteří si tvarem Země nejsou jisti, že se ten tvar dá snadno demonstrovat. Na konci si taky ukážeme nějaký experimenty, který si může vyzkoušet každej.
Obsah:
- Vzdálenosti
- Trvání letů letadel
- Mizení za horizont
- Západ slunce
- Dosvit slunce
- Vzdálenost slunce a měsíce
- Teplo slunce
- Pohyby slunce
- Jedna strana měsíce
- Zatmění měsíce
- Jižní souhvězdí
- Proč necítíme pohyb Země?
- Jak může na kulatej Zemi fungovat sextant?
- Jak to, že je na kouli odraz na hladině po celej dýlce od horizontu až k pozorovateli?
- Proč vidíme celej rok stejný hvězdy?
- Jak to, že nevidíme, že se budovy na obzoru naklání pryč od nás?
- Proč má měsíc jinou teplotu světla než slunce, jehož světlo údajně odráží?
- Proč nemusí letadla korigovat let natočením “čumáku” dolů, aby letěly v konstantní vejšce?
Blbosti, výmysly a lži lívanců
• “Neexistuje žádnej důkaz zakřivení Země”
• “Nikde neni vidět zakřivení horizontu zleva doprava”
• “Slunce mizí do dálky”
• “Slunce se přibližuje až úplně k horizontu”
• “Horizont je vždycky ve vejšce očí”
• “Dohled oka neni nekonečnej”
• “Světlo se na plochej zemi láme tak, že země/voda zakrejvá vzdálený objekty”
• “Když víc zazoomuješ na loď zpola zakrytou obzorem, ukáže se celá”
• “Vodní hladina je vždycky rovná, takže oceán na kouli nemůže fungovat”
- Země je prokazatelně kulatá
- Ověřit si to můžete sami
- Stínovej experiment
- Stínovej experiment 2
- Jak operujou lívanci
- Psychologická operace “Plochá Země”
Důkazy pro kulatou Zemi
Vzdálenosti
Jak bylo vysvětleno už v PZ1, na plochej Zemi absolutně nevychází vzdálenosti. Jakž takž odpovídaji na severní polokouli (čehož bylo využito v tej knize, na kterou jsem reagoval v PZ2), ale směrem od rovníku na jih se rozdíly mezi skutečnejma vzdálenostma a vzdálenostma na PZ zvětšujou geometrickou řadou. Na PZ má jižní polární kruh 6.7-krát větší obvod než ten severní.
Zatímco ve skutečnosti se od rovníku na jih vzdálenosti mezi poledníky zmenšujou, na PZ se zvětšujou. V Austrálii, Jižní Americe a jižní Africe máme víc než dvojnásobný rozdíly. Například vzdálenost ze severu na jih Austrálie (bez Tasmánie) tvoří ve skutečnosti 3/4 vzdálenosti ze západu na východ:
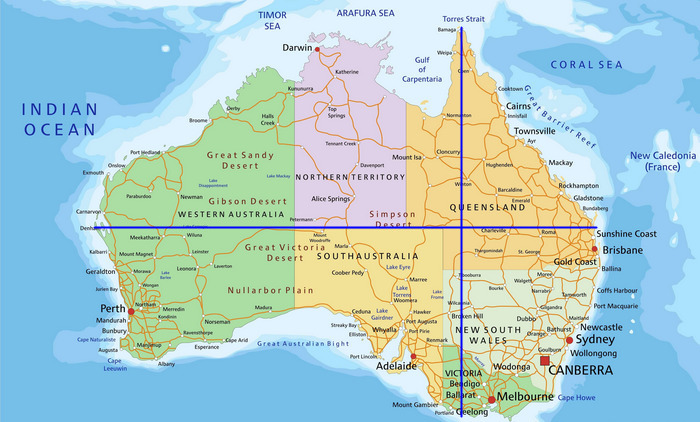
Na plochej Zemi je to ale jen zhruba 1/3, což je zatraceně velkej rozdíl.
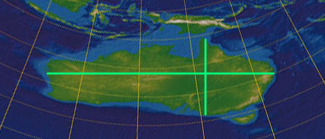
Tady vážně neni nijak těžký ověřit, jak to doopravdy je. Měření vzdáleností neni výhradou NASA nebo superbohatejch lidí. Máme třeba počitadla kilometrů v autech. Buď je šířka Austrálie 4000 km, jak je to změřený a vychází to na kulatej Zemi, nebo je to 9100 km, jak to zhruba vychází na plochej Zemi. To se dá zjistit, obzvlášť při takhle ohromnym rozdílu.
A to je jen jeden příklad. Pokud by byl pravdivej model plochý Země, tak by všechny vzdálenosti na světě byly změřený špatně. Jakou konspirací by se tohle dalo dokázat a utajit, nemám tušení.
Dnes máme GPS (kde mimochodem G znamená globální, neboli na kouli), systém, kterej, pokud vim, měří vzdálenosti dost přesně. A ty vzdálenosti odpovídaji kouli. Pokud by byla Země plochá, vzdálenosti z GPS by nikde neodpovídaly skutečnosti (řekněme kromě kolem severního pólu).
Takže jestli chcete věřit, že žijete na PZ, tak musíte věřit, že všechny data z GPS a veškerý jiný měření velkejch vzdáleností jsou špatně. Nebo by GPS nějak musel mít kilometry sever-jih jinak dlouhý než kilometry východ-západ a směrem k jižnímu pólu by se ty kilometry východ-západ musely postupně zvětšovat, zatímco ty sever-jih by zůstávaly furt stejný.
V Austrálii by si pak nikdo nesměl všimnout, že když jede rychlostí 100 km/h, tak ze severu na jih jede 100 km hodinu a z východu na západ jede 100 km přes dvě hodiny. Našťouchat reálný vzdálenosti do modelu PZ je prostě nemožný. Skutečný vzdálenosti jsou důkazem, že Země je kulatá.
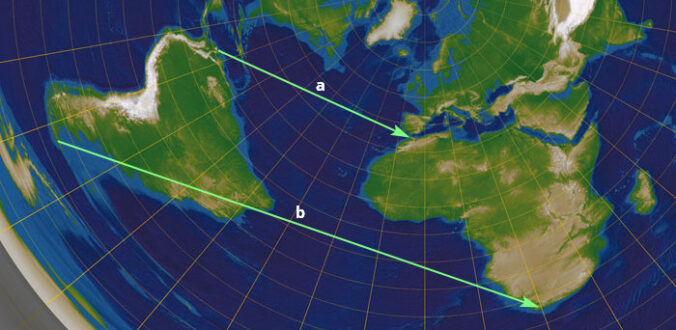
V PZ1 jsem ukazoval další příklad:
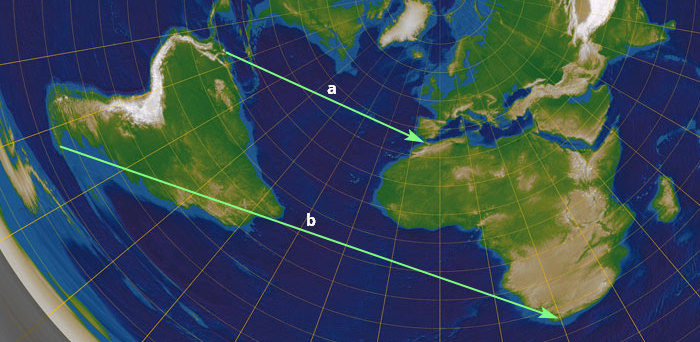
Vzdálenost a je ve skutečnosti větší než b, zatímco na PZ je b skoro 2.5x větší než a. Zároveň je na PZ Austrálie větší než USA, Kanada, a možná i Rusko (který je ve skutečnosti víc než dvakrát větší).
Fakt: Skutečný vzdálenosti vůbec neodpovídaji modelu PZ. Odpovídaji vzdálenostem na kouli.
Trvání letů letadel
To, že vzdálenosti na PZ nevychází, je snadno vidět i na tom, jak dlouho trvaji jaký lety letadel. Kdekoliv si vezmeme podobnou vzdálenost letů na severní a jižní polokouli, na PZ bude jižní vzdálenost aspoň dvakrát větší. Doba letu bude ale zhruba stejná, protože i vzdálenost je na kouli stejná. V PZ2 už jsem jeden příklad uved:
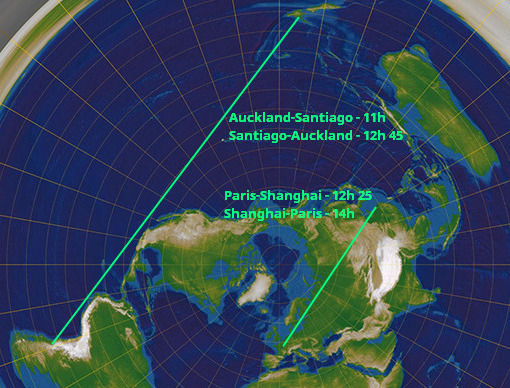
Tyhle dva lety jsou na kouli zhruba stejně dlouhý. Na PZ je Auckland-Santiago dva a půl krát delší. Ale letadlo ho zvládne ještě rychlejc než let Paříž-Šanghai. Vzdušný proudy dokážou vysvětlit tak maximálně20% rozdíl. Pokud let Paříž-Šanghai trvá kolem 13 hodin, měl by let Auckland-Santiago na PZ trvat kolem 32 hodin, takže řekněme, že 25 hodin by se jakž-takž dalo akceptovat, ale je totální nesmysl, aby to letadlo zvládlo za 11-12 hodin. Vyžadovalo by to dvakrát větší rychlost než jaký jsou ty letadla schopný.
Mimoto, jak poznamenal jeden pilot, kterej takový trasy běžně lítá (kromě toho, že potvrdil, že lítá kolem Antarktidy), tak ty letadla by na trasu Auckland-Santiago na vzdálenost podle PZ neměly ani s plnejma nádržema dostatek paliva.
Jak už jsem psal, můžete si to otestovat na www.flightconnections.com. Na mnoha příkladech si můžete vyzkoušet, že lety na jižní polokouli trvaji podobně dlouho jako stejně dlouhý lety na severní polokouli, ačkoliv na PZ by byly 2-3x delší. Lety jako Auckland-Santiago, Sydney-Santiago, nebo Johannesburg-Sydney, tak jak ve skutečnosti pravidelně probíhaji, by na PZ byly nemožný.
Skutečný lety letadel jsou konzistentní se vzdálenostma na kouli a ne na PZ.
Mizení za horizont
Jedním z nejlepších a nejjasnějších důkazů zakřivení Země je pozorování objektů mizících za horizont na moři s narůstající vzdáleností od nás. Na pevnině to bohužel moc dobře nefunguje, protože se dá těžko jasně oddělit zakřivení Země od kopců a údolí.
Na menších vodních plochách to taky moc dobře nefunguje, protože efekt atmosférický refrakce, kterou jsem vysvětlil v PZ1 (a kterou lívanci ve svejch experimentech nikdy nezapočítaji), je dost velkej a dovoluje vám vidět celkem daleko za skutečnej horizont. Zabejvat se vzdálenostma kolem 5 km teda nemá moc smysl. Neni ale třeba, protože máme místa, kde se města na břehu jezer daji pozorovat ze vzdáleností 20-80 km a zakřivení Země je tam jasně vidět.
Dobře si to můžeme ukázat na jezeře Michigan pozorováním Chicaga ze vzdáleností až 85 km.
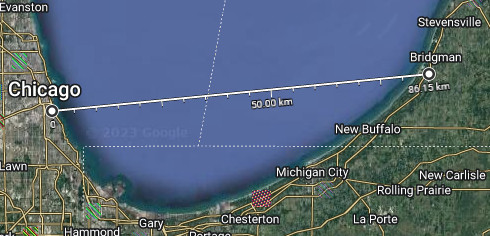
Když pojedete z Chicaga podél břehu jezera, postupně se vzdalujete a můžete Chicago pozorovat třeba z Indiana Dunes, Michigan City, New Buffalo, a někdy dokonce i města Bridgman, vzdálenýho 85 km. Jak se vzdalujete, vidíte z budov Chicaga míň a míň, až vám úplně zmizí z dohledu.
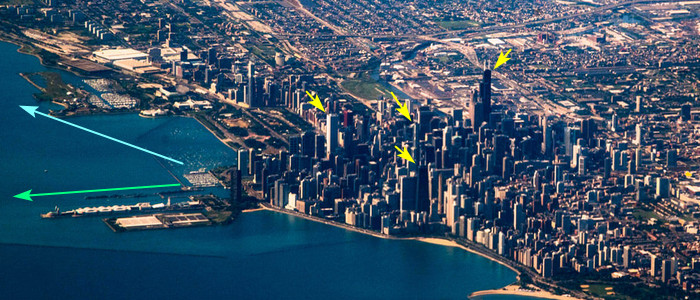
Kdo by to chtěl zkoumat víc do detailu, tady má dva pohledy ze vzduchu z různejch úhlů. Modrý šipky jsou směr Gary, zelený směr Bridgman. Žlutý šipky ukazujou nejvyšší budovy. Nejvyšší je Willis Tower (vícestupňová černá). John Hancock Center je druhá černá, která se nahoru zužuje a je na druhej straně města – z pohledu od jezera vpravo. Na obou jsou obvykle vidět dvě velký antény. Aon Center je bílá hranatá budova nejblíž k jezeru. Trumpův hotel je uprostřed a byl postavenej až 2009, takže na spoustě fotek chybí. Tady dole ukazuje svislá šipka, kde má bejt.

V roce 2020 byla postavená další hodně vysoká budova, St. Regis Chicago, mezi JHC a Aon, která se objeví jen asi na třech fotkách. Jelikož různý budovy jsou různě daleko od břehu jezera, jejich relativní vzdálenosti od sebe se mění s úhlem pohledu.
Našel jsem těch fotek hromadu a často spoustu ze stejný lokace. Na těch je velmi dobře vidět efekt tý refrakce za různýho počasí, protože někdy je ze stejnýho místa z věží Chicaga vidět mnohem víc než v jiný dny. Je teda běžný, že díky refrakci někdy vidíte z budov o desítky metrů víc než jindy.
Tenhle ohromnej efekt lívanci tvrdohlavě ignorujou, vypočítaji si na earthcurvature.com, kolik by toho na druhej straně “nemělo bejt vidět” a měří si něco na rybníku 5 km dlouhym a diví se, že věci pořád vidí. Přitom je dobře známý, že takhle díky atmosférickej refrakci můžete vidět třeba dvakrát dál, než byste měli podle výpočtu.
Je proto blbost se zabejvat malejma vzdálenostma, a hlavně pozorovat věci jen na jednu vzdálenost, protože je prakticky nemožný správně spočítat efekt tý refrakce (což lívanci nejen že neumí, ale ani se o to nikdy nesnaží).
Jedinej rozumnej postup je tudíž pozorovat jedno místo z různejch vzdáleností a srovnávat, co vidíme z menší dálky a co z větší. Pokud nám toho z větší dálky mizí za obzorem víc, neboli vidíme menší a menší část vršků budov, a pokud nám v nějakej vzdálenosti zmizí úplně, ačkoliv máme pořád dostatečný přiblížení, máme důkaz zakřivení Země. Takže si to vyzkoušíme.
V PZ1 jsem už ukázal příklady lodí, Toronta, nebo Lake Pontchartrain, takže na ty se můžete kouknout tam. Tady si dáme Chicago.
Chicago z 16 km:

Chicago z 24 km:

Už tady vidíme jasnej rozdíl. Nízký široký budovy nám úplně zmizely. (Tohle neni ze břehu, ale z jezera, z východního směru, proto to má jinej úhel než následující fotky.)
Chicago z 35 km:

Tohle je jedna z těch novějších fotek, kde je vidět víc budov, což je vidět hlavně ve srovnání s tou další. (Trump Hotel je v zákrytu s Aon Center – jak se budeme vzdalovat a měnit úhel pohledu, budou se od sebe oddělovat.)
Chicago ze 40 km:


Chicago z 45 km:

Tady je patrnej efekt refrakce, takže budovy vypadaji vyšší, než by měly.
(Taky je tu St. Regis Chicago a další nový budovy.)
Chicago z 51 km:

Ve vzdálenosti 51 km je národní park Indiana Dunes a odtud se najde fotek hodně, takže těch si ukážeme víc. Všimneme si, že i z tý jedný vzdálenosti je toho někdy vidět víc a někdy míň. Částečně je to proto, že některý fotky jsou focený přímo z pobřeží a některý z nějakýho trochu vyššího místa dál od břehu. Druhej rozdíl je právě ta refrakce, která se mění v důsledku různejch teplot a dalších faktorů.
Nemá teda vůbec smysl se pokoušet zabejvat tim, kolik metrů by z jaký věže “mělo bejt” odkud vidět, protože je to ve skutečnosti pokaždý jinak i ze stejnýho místa a je hodně těžký to správně spočítat. (Mimochodem to, co si spočítáte na tej kalkulačce, platí jen při pohledu z úrovně země. Jakmile stojíte a díváte se teda z vejšky 150-170 cm, vidíte toho mnohem víc. A pokud stojíte ještě vejš, tak tuplem.)
Hlavní, co by se mělo sledovat, je to, jestli obecně z větší vzdálenosti nám z toho města mizí víc a víc, odspoda nahoru, až ho z nějaký vzdálenosti nevidíme vůbec, což je přesně to, co by se mělo stát na zeměkouli, ale nemůže se stát na PZ.
Chicago z Indiana Dunes, 50-52 km:

^ Tady vidíme velkou míru zkreslení v pruhu těsně nad hladinou v důsledku refrakce, takže to vypadá, že je vidět o dost větší část budov než na většině ostatních fotek. Nejen že je tu vidět “dál za horizont”, ale ještě se tu část zrcadlí.




(Tohle je další novější fotka, na kterej je minimálně 8 novejch budov, který na ostatních nevidíme.
Pět nejvyšších zleva doprava je Willis, Aon, Trump, St. Regis, Hancock.)



Tady na konci máme dvě fotky (plus výřez ze třetí), kde vidíme slunce tak akorát dotýkat se hladiny. Efekt atmosférický refrakce je tak velkej, že když za běžnejch podmínek (opět záleží na teplotě, tlaku atd.) vidíme slunce, jak se spodním okrajem dotýká vodní hladiny, tak je ve skutečnosti už za obzorem a naopak se tý hladiny tak akorát “dotýká” horním okrajem (takže bez atmosféry by nebylo vidět).
Neboli to slunce, který vidíte na těch posledních fotkách, je ve skutečnosti už pod obzorem a vidíte ho jendíky atmosférickej refrakci. To nám dává nějakou představu o tom, jak ohromnej ten efekt může bejt.
Je ale nutný poznamenat, že na ty budovy to tak velkej efekt mít nebude, protože na to slunce koukáme ještě skrz další tisíce kilometrů atmosféry za tim městem, a tudíž u něj je ten efekt mnohem větší než u toho města, na který koukáme jen skrz 51 km. Je ale důležitý vědět, že s tim efektem refrakce je třeba počítat. Na poslední fotce vidíme i to, že spodní čtvrtina slunce patří ve skutečnosti níž než ji vidíme.
Chicago z 60 km:


Tady už nám zmizela většina budov a vidíme jen špičky těch nejvyšších.
Chicago ze 72 km:

Tady můžeme dokonce srovnat, jak ty budovy vypadaji vedle slunce ze 72 km a z 51 km.



Z týhle vzdálenosti vidíme ještě větší efekt refrakce (protože čím níž u země/hladiny, tím je větší, a teď už koukáme jen na tenkej pruh špiček budov, těsně nad hladinou a s větším přiblížením). Někdy je vidět asi 20 budov, někdy už jen několik těch nejvyšších. Hlavně je ale evidentní, že ze 72 km vidíme zřetelně menší část a množství budov než z 51 km, kde jich bylo vidět možná sto. Většinu z nich už tu nevidíme.
Chicago z 80 km:

Chicago z 85 km:

85 km je vzdálenost, ze který je Chicago vidět jen málokdy, proto se už nedá najít moc fotek. Někdy ale vidět je. Je ale evidentní, že naprostá většina je bezpečně schovaná za horizontem kulatý Země.V poslední fázi už jsou vidět jen špičky asi 4 nejvyšších budov.

Když se ale poštěstí a nahrávaji tomu atmosférický podmínky, dá se výjimečně z těch 85 km vidět tohle. To nám opět ukazuje, že atmosférická refrakce může do ohromný míry změnit výsledky experimentů. Lívanci ji nikdy neberou v úvahu a stále dokola vykřikujou, že maji “důkaz” plochý Země, protože vidí něco, co vidět “nemaji”. Nemaji to ale vidět na Zemi bez atmosféry. Ta naše ji fakt má.
Z větší vzdálenosti už fotky Chicaga asi nenajdete. Přitom na jezeře Michigan můžete bejt třeba 200 km od Chicaga a nemít v cestě nic než vodu. Tak jak to, že Chicago nevidíme odtud? Lívanci sami jako další “důkaz” PZ uvádí, že je možný vidět Alpy z Pyrenejí, což je 400 km daleko. Tak proč nevidíme přes Lake Michigan Chicago na 200 km? Nebo aspoň na 100 km? Dalekohledy a kamery máme dobrý.
Koneckonců na tej poslední fotce vidíte, že když to Chicago vidět z 85 km je, máme pořád dostatečný přiblížení, abysme ho viděli úplně zřetelně. Rozhodně neni na hranici “zmizení do dálky”. Takže by mělo bejt v pohodě vidět ze 100 km, pokud jde o přiblížení a velikost.
Ve skutečnosti ale neni většinou vidět už z těch 85 km, ačkoliv dostatečnej zoom evidentně máme.
Podle oblíbený kalkulačky lívanců by na 85 km mělo Chicago bejt nějakejch 566 metrů pod obzorem. Neboli budovy nižší než 566 metrů by “neměly bejt vidět”. (Nicméně z místa 170 cm nad zemí (jako třeba když normálně stojíte a nemáte držku přilepenou na zemi) už je to jen 506 metrů, takže 60 metrů rozdíl.) Willis Tower je 442 m vysoká (bez antén), takže bez atmosféry by byla přes 120 metrů pod horizontem. Většinou z týhle vzdálenosti vidět neni, ale někdy jo, a jak vidíme, je z ní někdy vidět možná 100 metrů i víc (ta horní část, nad posledním “schodem”, má něco přes 80).
Když ta budova je někdy za obzorem a někdy je z ní vidět 100 metrů, můžeme buď tvrdit, že se zakřivení Země mění ze dne na den (pokud jsme dementi), nebo můžeme pochopit, že atmosférická refrakce nám může na 85 km ukázat něco, co by bez atmosféry bylo 200 metrů pod obzorem.
I když nám to takhle ukáže mnohem víc, než bysme viděli bez atmosféry, pořád se z toho nijak nedá usuzovat, že Země je plochá, protože 3/4 tý největší budovy je jasně za obzorem a většina budov je za obzorem úplně. A jelikož tu máme důkaz, že na to město “dohlídneme”, a přesto z něj většinou i za dobrýho počasí neni vidět nic, je evidentní, že je obvykle schovaný za horizontem celý, zatímco na PZ by mělo bejt celý vidět.
Tady máme teda naprosto jasný důkazy zakřivení Země. Když lívanci tvrdí, že “žádný důkazy zakřivení Země neexistujou”, tak lžou.
Západ slunce
Tenhle bod souvisí s tím předchozím a už byl detailně vysvětlenej v PZ1. Skutečnost, že slunce mizí za horizont, což by se na PZ nikdy nemohlo stát, je jasnym důkazem zakřivení Země. Žádnej lívanec mi nedokázal předložit žádnej argument, kterej by to zpochybnil. Nejlepší, na co se zmohli, jsou naprosto stupidní žvásty o tom, že “slunce mizí do dálky”, což je evidentně v rozporu s pozorováním a tudíž lež.

Stručně shrnuto: Na PZ by se spodní okraj slunce nikdy nemoh dostat pod úroveň horizontu na moři.
Kdo nepochopí tohle, tomu asi neni pomoci:

Dosvit slunce
Dalším nesporným důkazem, že model PZ nefunguje, je to, kam slunce dosvítí a kam ne. Na PZ má slunce 51km v průměru a je asi 5 tisíc km nad zemí. Neexistuje žádnej způsob, jak by takový slunce mohlo osvítit takovou část Země, která je ve skutečnosti osvícená.
V první řadě, timhle způsobem by bylo nemožný mít den a noc. Mohli bysme mít světlejší a tmavší část, ale přechod by byl plynulej a ta tmavší část by měla k noční tmě zatraceně daleko. A lokální slunce nad PZ nemůže absolutně nijak dosáhnout toho, že na jednom místě je normálně vidět a jen o pár stovek kilometrů dál je tma.
Můžete si vzít mapu tý PZ (nebo to prostě otestovat na podlaze bez mapy), nějakou menší žárovku nebo jinej zdroj světla, kterej neni nijak stíněnej a svítí na všechny strany (jako slunce), a zkusit, jestli se vám podaří na tej mapě nebo zemi dosáhnout toho, že na nějakym místě bude jasný světlo a o pár centimetrů dál úplná tma.
Nepodaří se vám to, protože to nejde. Položte třeba človíčka z lega na zem někam, kde na něj jasnědopadá světlo. I když dáte dalšího dvakrát dál od zdroje světla, bude na něj pořád dopadat slušný množství světla, a hlavně bude evidentní, že z toho místa, kde stojí, bude ten zdroj světla jasně vidět. Nikde nebude hranice, za kterou by byla tma.
Nebo když to podám jinak – zkuste si v úplně temnej místnosti (komora bez oken nebo třeba koupelna) jakymkoliv nestíněnym světlem, který svítí na všechny strany, nasimulovat den v půlce místnosti a noc ve druhej. Je to jednoduchej experiment, kterej zvládne kdokoliv.
Zjistíte samozřejmě, že to nejde. Bude-li půlka místnosti jasně osvětlená, tma nebude nikde. Podaří-li se vám to světlo mít natolik tlumený, aby byla v části místnosti tma, jasný světlo bude tak možná pár centimetrů kolem zdroje, jestli vůbec to. Kdokoliv věří modelu lokálního slunce, absolutně nechápe, jak funguje světlo.

Lívanci si to představujou nějak jako na tomhle obrázku. Žlutá tečka je zdroj světla ve tmavej místnosti (velikost a vejška nad zemí tu poměrově zhruba odpovídaji modelu PZ). Slunce svítí vždycky přesně na polovinu Země, takže tohle světlo by muselo svítit přesně na polovinu místnosti (s přechodem maximálně pár centimetrů). A ještě by ta hranice musela bejt rovná a ne zakřivená! Nechápu, jak si někdo může myslet, že takhle funguje světlo, když si kdykoliv může vyzkoušet, že nefunguje.

Tady vidíme, jak funguje světlo doopravdy. Se vzdáleností od zdroje slábne postupně. Podle modelu PZ by ale napravo od oranžový čáry mělo bejt všude světlo a nalevo všude tma. A proč má ta rozdělovací rovná čára jít zrovna timhle směrem a ne nějakym jinym, vám nikdo nepoví.
Snadno si taky vyzkoušíte, že když se budete od toho světla vzdalovat – a řekněme, že nám experiment dovolí se vzdálit hodně daleko, třeba dvacet metrů – tak dojde mnohem dřív k tomu, že budete v relativní tmě, než k tomu, že už neuvidíte to světlo. Na tom obrázku s autem a sluncem vidíte, jak to vypadá, když se vzdalujete od zdroje světla, versus jak vypadá západ slunce. A na obrázku se žárovkou vidíte, že v jeho levym rohu je celkem tma, ale je vám naprosto jasný, že z toho místa tu žárovku uvidíte úplně zřetelně. Rozsvícenou žárovku uvidíte v noci na kilometr, ale kolem vás světlo z ní nebude!
Když se budete v jinak tmavym prostoru vzdalovat od jedinýho zdroje světla, tak to světlo pořád zřetelně uvidíte i v bodě, kdy už budete stát ve tmě. Při západu slunce se ale děje opak. Slunce už nevidíte, ale kolem vás je pořád světlo.
Tohle se teda dá demonstrovat úplně jednoduchym experimentem, s naprosto jasnym výsledkem, kterej jasně vyvrací model PZ.
To, že po západu slunce je kolem nás pořád světlo, je proto, že slunce je pořád stejně daleko a skrz atmosféru k nám nějaký světlo dopadá, ačkoliv je slunce už za obzorem. Podobnou situaci si můžete vyzkoušet doma v noci. Váš partner drží zdroj světla – v místnosti je světlo. Partner zajde se světlem těsně za roh – v místnosti je pořád dost světla, i když vy jeho zdroj už nevidíte.
Na PZ se ale slunce nemá za co schovat. Údajně “mizí do dálky”. Pak byste ho ale viděli ještě hodně dlouho potom, co se vzdálilo natolik, že vy už stojíte ve tmě – přesně tak, jako vidíte v noci na obloze hvězdy, ačkoliv je kolem vás tma. Hvězdy nám ukazujou, jak vypadá světlo, který je tak daleko, že už prostor kolem nás neosvítí. Ale ty hvězdy pořád vidíme.
V reálnym světě pozorujeme, že sluncem je vždycky osvětlená přesně polovina Země. Na kouli je to naprosto jasný. Na placce je to naprosto nemožný. Jak si můžete jednoduchym experimentem ověřit, nikdy se vám nepodaří mít ve vzdálenosti X od zdroje světla totální světlo, a zároveň ve vzdálenosti 2X totální tmu. Takhle se prostě světlo nechová.
Pro model PZ neexistuje žádná varianta toho, kam slunce dosvítí, která by dávala smysl a odpovídala realitě. Světelná koule svítí na všechny strany stejně, takže dosvit slunce na ploše by měl bejt nějakej kruh, ačkoliv, jak už jsme viděli, ten kruh nikdy nebude mít žádný jasný ohraničení.
Máme tu ale třeba taky ten problém, že v létě je slunce vidět všude za severním polárním kruhem a v zimě za jižním. Polární den v Antarktidě můžete vidět třeba tady, tady, nebo tady. Všimněte si směru, kterym se točí stíny. To na PZ nefunguje:
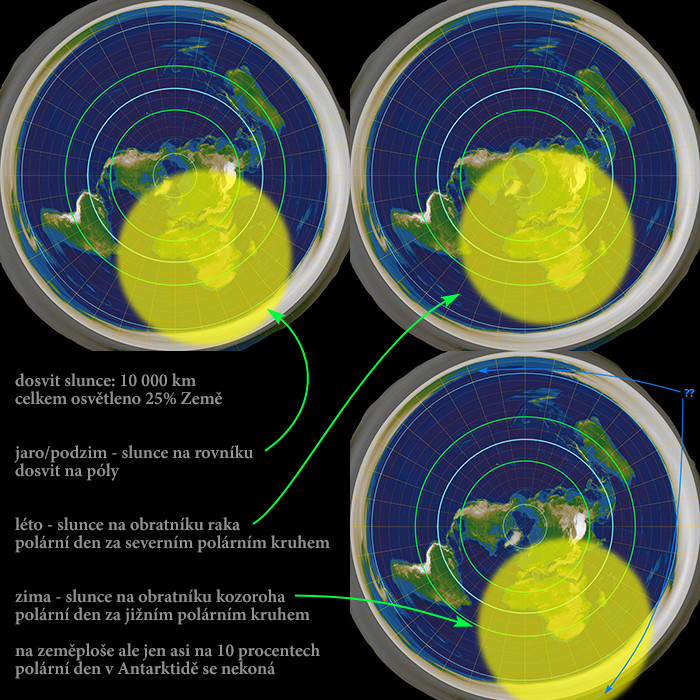
Samozřejmě “dosvit slunce 10000 km” je samo o sobě blbost, jak bylo vysvětleno, a pokud 10000 km od slunce bude “den”, tak 20000 km od něj bude pořád slušně vidět, a hlavně uvidíte to slunce.
Další problém tady je to, že v tejhle ukázce slunce neosvětluje 50% Země, ale jen 25%, což očividně neodpovídá realitě. Když si to ale zkusíme představit tak, aby slunce osvětlilo 50% Země tak, jak se to opravdu děje, je to na PZ totální absurdita.
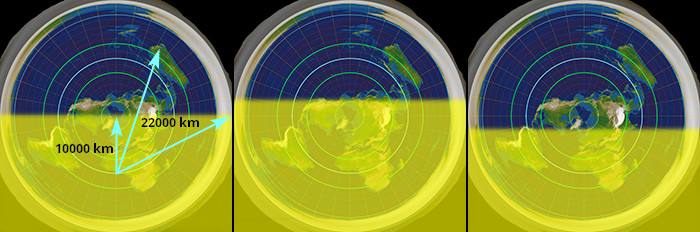
Znamenalo by to v první řadě, že dosvit slunce je v různejch směrech různej, což nemá žádný racionální vysvětlení. A když to slunce posuneme z rovníku na obratníky, je to totální chaos, kterej nemá s realitou nic společnýho. Celej tenhle model je totální hovadina, která neni ani trochu promyšlená.
Můžeme se na to dívat z jaký strany chceme a nikdy to nevyjde. Momentálně (ke konci května) slunce vychází kolem 5 hodin a zapadá kolem 9 večer. Bez letního času teda slunce svítí od 4 ráno do 8 večer, neboli 16 hodin je světlo a 8 tma. Takže nějak takhle:
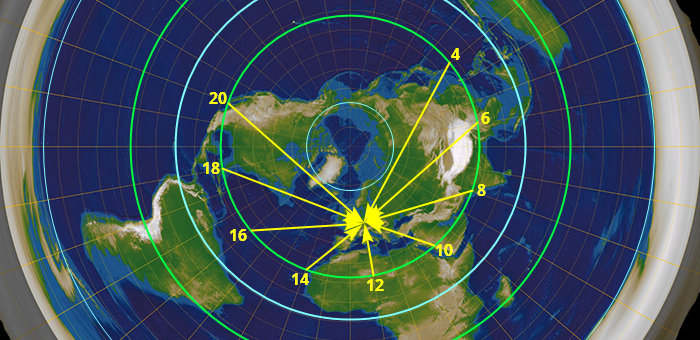
Slunce ještě neni na obratníku (to až tak za měsíc), takže ten rozptyl je ještě větší. Když se teda podíváme, kde je slunce ve 4 ráno a nakreslíme si kruh, aby dosvítilo k nám, vypadá to nějak takhle:
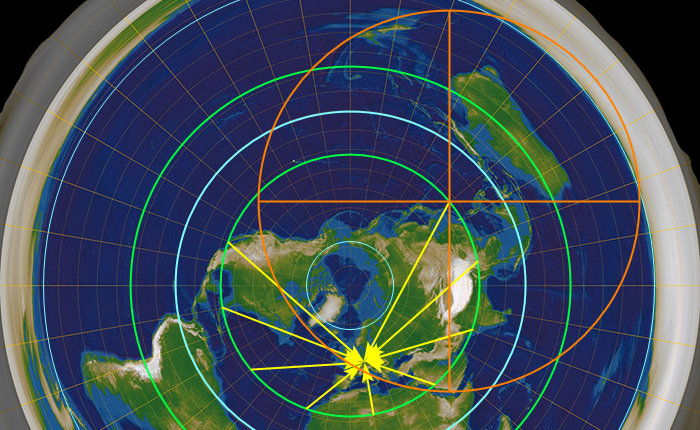
Jelikož slunce ještě neni na obratníku, kruh by byl ve skutečnosti větší. Na druhou stranu za měsíc bude den ještě delší, takže to slunce k nám bude muset svítit z ještě větší části kruhu. Co tady vidíme? Vidíme, že ve 4 ráno je den v celej Asii, celej Austrálii, většině Evropy, a části Severní Ameriky, včetně asi půlky Kalifornie. Což se nikdy neděje.
Zároveň je v Evropě světlo a v Africe tma, což se taky nikdy neděje, stejně jako nemůže bejt světlo v Kanadě a Kalifornii a tma v Mexiku. A jak to vypadá v poledne?
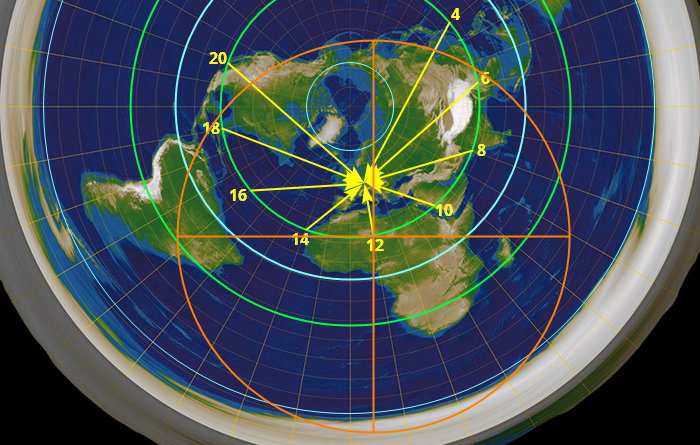
Světlo v celej Asii, Evropě, Africe, a většině Severní Ameriky. Ačkoliv Florida má světlo, většina Jižní Ameriky, která je víc na východ, světlo nemá. Nic z toho neodpovídá realitě.
A tohle je slunce na severní polokouli, kde je to pro PZ mnohem příznivější. Teď si to představte na Falklandách, který maji stejnou zeměpisnou šířku jako my, ale na jihu, a se sluncem na druhym obratníku. Vymyslete, jak bude slunce svítit 16 hodin tam.
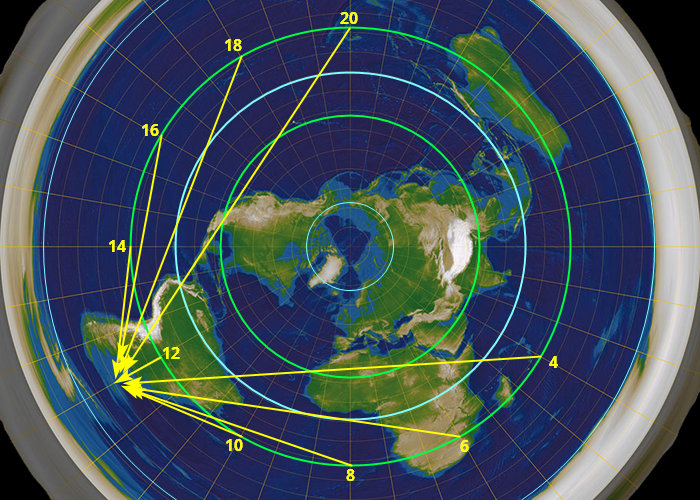
Hodně štěstí. (Úhly taky parádní, že?)
Vidíme teda, že dosvit slunce nám ukazuje hned několik důvodů, proč model PZ neni pravdivej. Je to další jasná demonstrace toho, že Země je koule a ne placka. Jasný jak facka.
Vzdálenost slunce a měsíce
Přesnou vzdálenost slunce od Země jsem od lívanců nezjistil, ale můžeme si to celkem snadno spočítat. Budeme vycházet ze situace, kdy stojíme na rovníku a je poledne, takže slunce máme přímo nad sebou. Naše slunce je 150 mil. km daleko a má 1392 tisíc km v průměru. Jelikož slunce vidí melouni i lívanci stejně velký a lívanci nám tvrdí, že má 51 km v průměru, tak si trojčlenkou lehko spočítáme, že to jejich je zhruba 5500 km daleko.
Problém je, že na PZ by z různejch vzdáleností mělo vypadat různě velký, ale ve skutečnosti vypadá furt stejně (protože je ve skutečnosti pořád stejně daleko). Tady jsem načrtnul model, kdy sledujeme slunce v poledne (kratší šipky) a při západu (delší) z různejch míst v různý roční období:
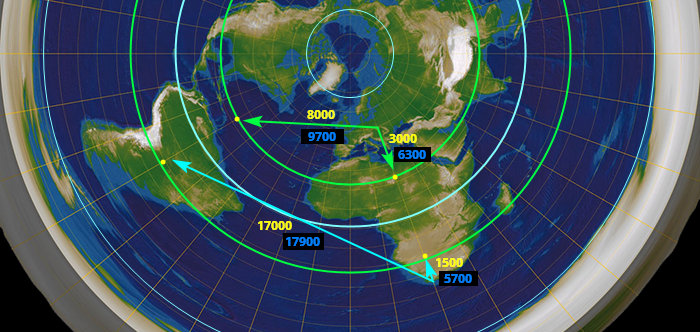
Žlutý jsou vzdálenosti “na mapě”; modrý jsou “skutečný”, tj. včetně tý vejšky 5500 km nad zemí. Místa pozorování jsou tam, odkud vychází šipky. Jak vidíme, ze zelenýho místa je slunce při západu zhruba 1.5x dál než v poledne, zatímco z modrýho místa je při západu víc než 3x tak daleko, jako v poledne.
(Poznámka: Kdyby někdo nechápal, kde beru ty vzdálenosti, a myslel si, že si je vymejšlim, tak jsou všechny odvozený od faktu, že od pólu k rovníku je 10000 km. Můžete si je teda ověřit pravítkem na obrazovce. Když vám pól-rovník dá třeba 5 cm, máte měřítko 5 cm = 10000 km.)
Nejen že by teda při západu mělo slunce vypadat o dost menší než v poledne, ale ten poměr je pokaždý jinej, v rozmezí minimálně 1.5-3 ku jedný. Slunce vidíme ale odkudkoliv na Zemi ve kteroukoliv denní dobu zhruba stejně velký. Rozdíly můžou bejt nanejvejš pár procent v důsledku refrakce, ale rozhodně nikdy nevidíme slunce dvakrát nebo dokonce třikrát větší, než jindy. Stejně tak měsíc.
To, že slunce ve vzdálenosti 18000 km vypadá stejně velký jako ve vzdálenosti 5500 km, je očividná blbost a model lokálního slunce to opět spolehlivě vyvrací. Slunce vypadá vždycky zhruba stejně velký, protože je vždycky zhruba stejně daleko.
Teplo slunce
Všichni (s výjimkou snad jen pár extrémních případů) víme, že když svítí sluníčko, je teplo. Je evidentní, že slunce hřeje. Když koukám na předpověď počasí, tak rozdíl mezi nočníma a denníma teplotama v jeden den je tak 6-13°C. To znamená, že slunce přes den zahřeje Zemi až o 13 stupňů a někdy i víc. Takže hřeje fakt hodně.
V čem že je problém? Melounský slunce je 109x větší než Země. Zeměplošský slunce je 784x menší než Země. Když si to ukážeme názorně, vypadá to asi takhle:
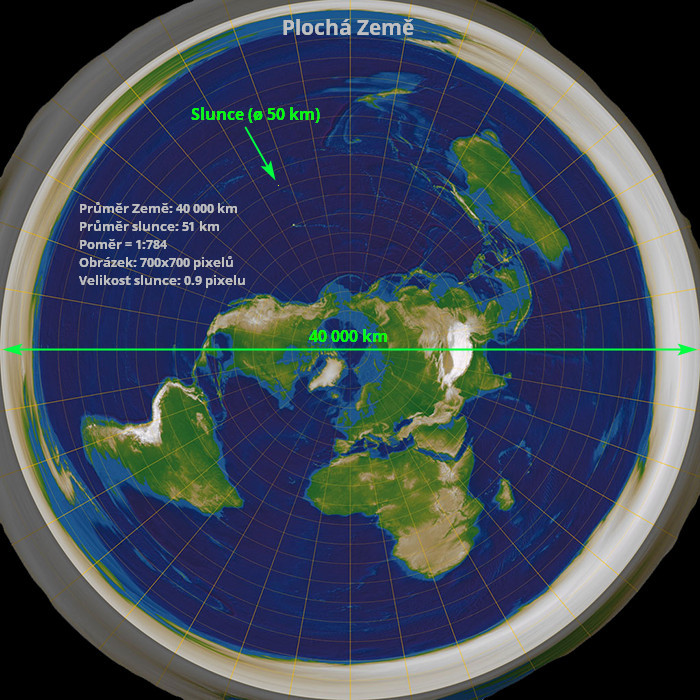
Nebudu to předkládat jako jasnej “důkaz”, ale představa, že tahle malá tečka zahřeje stovky miliónů čtverečních kilometrů o deset stupňů, nebo i víc, a za miliardy let jí ještě nedošla energie, mi připadá mírně (a slušně) řečeno značně nerealistická. Je to ale ještě horší, když se místo poloměru podíváme na objem. Naše 150 miliónů km vzdálený slunce má objem 1 300 000 krát větší než Země. Lívancový slunce má objem 15 650 000 krát menší než (kulatá) Země. Vážně tahle kulička ohřívá Zemi? A opět to, že zahřívá jen půl Země, nedává smysl. Dosah tepla, stejně jako světla, nemá takhle úzký hranice.
Pokud si to chcete představit v menším měřítku, představte si místnost o rozměrech 3×3 metry (takovej normální pokoj). To reprezentuje Zemi. Zeměplošský slunce by tu představovala kulička o velikosti skoro 4 mm, vznášející se asi 40 cm nad podlahou. A díky tejhle svítící kuličce bude v půlce místnosti světlo a v půlce tma, a v půlce teplo a v půlce zima. To je ale kravina, co?
A samozřejmě ta kulička tam bude běhat do kolečka a vždycky na jednej straně místnosti bude podlaha znatelně teplejší než na druhej. Fakt nechápu, jak se skrz všechny tyhle nesmysly udržuje teorie PZ při životě.
Pohyby slunce
Jak jsem popsal v PZ1, pohyby slunce (a měsíce a planet) na PZ jsou naprosto bizarní. Slunce “obíhá” kolem pomyslnýho bodu 5500 km nad severním pólem (proč?), půl roku se pomalu posunuje od jednoho obratníku ke druhýmu (proč?) a postupně zrychluje (proč?), a druhejch půl roku se posunuje zpátky a zpomaluje. Při zimním slunovratu obíhá 1.7x rychlejc než při letním.
Nic z toho neni nijak vysvětlený. Co ho drží ve vzduchu, proč se pohybuje, co mu dodává energii, proč lítá do zatáčky, proč se poloměr oběhu každej den mění, proč zrychluje a zpomaluje, proč na obratnících mění směr, atd. “Lokální slunce” neni ani model nebo teorie. Je to jen směšnej výmysl.
Kromě toho, že mi nikdo zatim nedokázal vysvětlit, proč se cokoliv z toho děje, to slunce by potřebovalo nepředstavitelný množství energie jak na to, aby se drželo ve vzduchu a lítalo dokolečka podle nějakýho sofistikovanýho nevysvětlitelnýho vzorce, tak na to, aby svítilo a vyzařovalo masivní množství tepla.
Jedna strana měsíce
Jsou věci, který lívanci nemůžou popřít, ačkoliv tyhle věci zároveň popíraji jejich “model”. (A tak o nich radši nemluví.) Jednou z nich je fakt, že vždycky vidíme jen jednu stranu měsíce. To je na PZ nemožný.
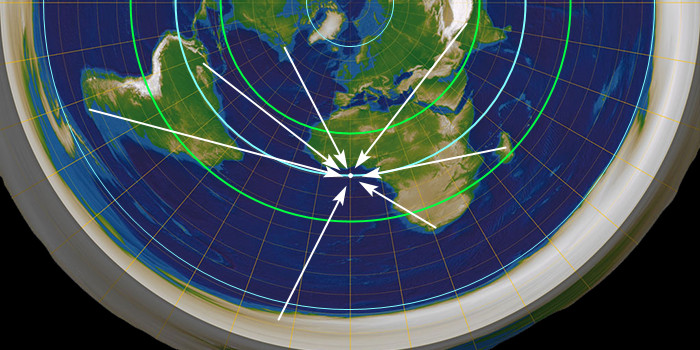
Pokud je měsíc jen nějakejch 5 tisíc km nad Zemí, lidi na něj koukaji ze všech možnejch směrů, jak je vidět na obrázku. Jelikož se dá vidět až z 20 tisíc km a přitom je jen 5 tisíc km nad Zemí, dá se na něj dívat z úhlu asi 15°. To znamená, že by v jednu chvíli bylo z různejch míst na Zemi vidět dohromady asi 90% měsíce. Je ale vždycky vidět jen 50%.
A tím se můžeme s modelem blízkýho měsíce a PZ rozloučit. Vidět odkudkoliv vždycky jen jednu stranu lokálního měsíce je nemožný. Měsíc je teda hodně daleko. Potom ale nemůže “obíhat nad plackou”, protože by se neměl kam 12 hodin denně schovávat. To funguje jen na kouli.
Zatmění měsíce
Zatmění měsíce neni na PZ možný, protože Země nemůže měsíc zastínit, neboť se nikdy nemůže dostat mezi něj a slunce. Nechám na lívancích, ať vám vysvětlí sami, jak to, že máme zatmění měsíce. Jestli od nich někdo dostanete vysvětlení, který vám bude dávat smysl, dejte mi vědět.
(Ono by reálně nevycházelo ani zatmění slunce, ale to už je na větší výpočty, takže to nebudeme řešit, protože lívanci nezvládaji ani jednoduchý výpočty.)
Jižní souhvězdí
Jižní polokoule je pro PZ neřešitelnym problémem z mnoha důvodů. Zajímalo by mě, kolik lívanců tak asi žije v Austrálii, protože z jejich pohledu ty zeměplošský bláboly už vůbec nedávaji smysl. Jednim z mnoha fenoménů, který tam ani trochu nefungujou, je pohyb hvězd po noční obloze.
Jak asi všichni ví, na severní polokouli máme Polárku, hvězdu, která je téměř přesně severně od Země. Při pozorování noční oblohy se hvězdy pohybujou od východu k západu, jako slunce a měsíc, ale Polárka se prakticky nehejbe, neboť je to severní nebeskej pól.
Na jižní polokouli to funguje podobně – je tam jižní nebeskej pól, kterej je pořád na stejnym místě a kolem kterýho se ostatní hvězdy “točí”. Když koukáme na severní polokouli na Polárku, hvězdy se kolem ní točí z našeho pohledu proti směru hodinovejch ručiček. Na jižní polokouli to funguje naopak. Hvězdy se kolem jižního nebeskýho pólu točí po směru hodinovejch ručiček.
Jih nemá na pólu žádnou významnou hvězdu, ale nedaleko něj je Jižní kříž, kterej se používá pro navigaci podobně jako Polárka. Stejně jako na severní polokouli je Polárka vždycky vidět na severu, na jižní je Jižní kříž vždycky vidět na jihu.
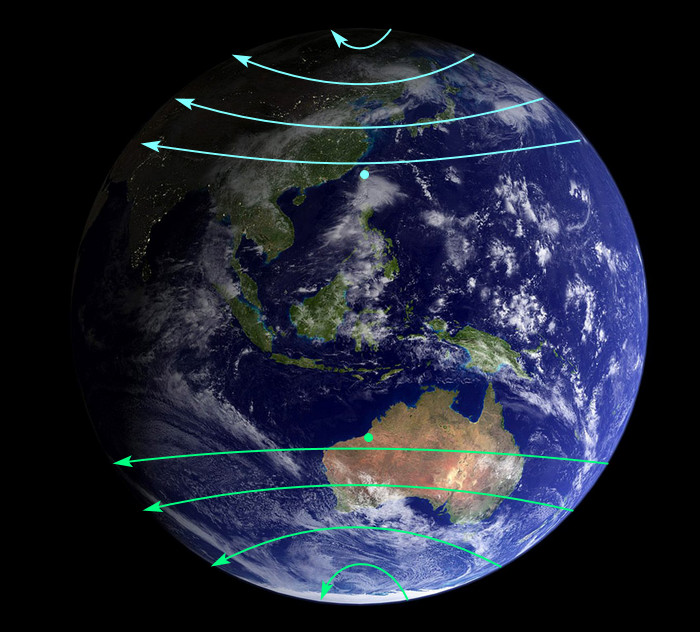
Takhle nějak vidíme trajektorie hvězd, když se z místa na severní polokouli díváme na sever, a z místa na jižní polokouli na jih. Čím blíž jsou hvězdy k pólu, tím menší je kruh, po kterym je vidíme obíhat. A jelikož je ten směr oběhu důsledkem otáčení Země, která se točí jednim směrem, ale na protějších polokoulích se k jejich pólům díváme opačnými směry, směr rotace hvězd kolem severního pólu je opačnej než kolem jižního.
Tohle neni žádná složitá věda. Každej to uvidí, když bude sledovat oblohu. Zároveň platí, že Polárku vidíme odkudkoliv na severu Země a Jižní kříž vidíme odkudkoliv na jihu. To jsou nezpochybnitelný fakta.
Stejně nezpochybnitelný je, že na PZ to ani trochu nefunguje.
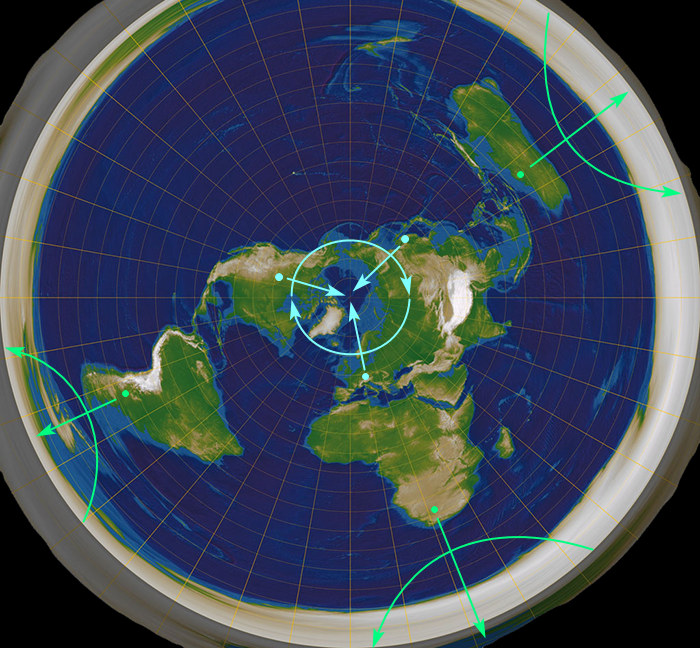
Na severu nám to jakž takž vychází. Zakřivený šipky ukazujou, jak obíhaji hvězdy z pohledu modrejch teček, a rovný šipky ukazujou, kterym směrem vidí modrý tečky Polárku. (Nicméně by to ve skutečnosti nevycházelo ani tam, protože na PZ ty hvězdy nejsou moc daleko/vysoko, takže na ně ze Země koukáme pod nějakym ostřejším úhlem, a tudíž by nám neobíhaly v kruhu, ale po elipse. Jelikož jsou ve skutečnosti zatraceně daleko, vidíme jejich trasy jako kruhy, viz níže.)
Zelený zakřivený šipky nám ukazujou, jak vidí hvězdy obíhat pozorovatelé ze zelenejch teček, a rovný šipky ukazujou, kde ti pozorovatelé vidí Jižní kříž, respektive hlavně jižní nebeskej pól. Všichni ho vidí na jihu. Je evidentní, že tenhle model Země je naprostá hovadina, která v žádnym případě neodpovídá realitě a běžnýmu pozorování.
Je to opravdu velmi jednoduchý. Všichni na jižní polokouli vidí jižní nebeskej pól na jihu, a ten pól se nehejbe. To je fakt, ze kterýho lívanci nemaji kam vybruslit.
Plochá Země ve skutečnosti nemá žádnej jižní pól. Na obloze ale vidíme jižní nebeskej pól, tj. místo, kolem kterýho obíhá vše ostatní na obloze. Je to místo, kam míří zemská osa. Na PZ by takový místo nemohlo existovat.
Pokud by si někteří tvrdohlaví a natvrdlí jedinci chtěli namlouvat, že ty zelený šipky můžou zakřivit na druhou stranu, tak nemůžou. Rovný šipky ukazujou na střed toho otáčení. Na severu ukazujou na Polárku, a pozorováním víme, že ostatní hvězdy obíhaji kolem ní, což ukazujou ty zakřivený šipky.
Stejně tak zelený rovný šipky ukazujou na jižní nebeskej pól (nebo teda kde by měl z pohledu zelenejch teček bejt na bázi skutečnýho pozorování), kterej je středem oběhu všech jižních hvězd. Zakřivený šipky musí teda kroužit kolem toho pólu. Pokud bysme křivky obrátili, aby hvězdy obíhaly jako měsíc, obíhaly by i ty jižní kolem Polárky, což se evidentně neděje.
 Sever
Sever
 Jih
Jih
Samozřejmě hvězdy ve skutečnosti obíhaji stejnym směrem jako měsíc a pohybujou se zároveň s nim, což ale na PZ neni možný, protože by pak Jižní kříž musel obíhat po vnějšku zeměplochy delší trasou než ostatní souhvězdí, což nedělá, neboť dělá opak a má trasu kratší.
Na obloze vidíme, že se hvězdy pohybujou zároveň s měsícem, kterej na PZ obíhá kolem severního pólu. Hvězdy na jižní polokouli ale obíhaji kolem jižního pólu, kterej na PZ ani neexistuje. PZ nedokáže nijak vysvětlit fakt, že na jižní polokouli se pozorovaný hvězdy točí opačnym směrem než na severní.
Pozorování hvězd z jižní polokoule odpovídá modelu zeměkoule a nedá se napasovat na PZ.
Mimochodem, na rovníku jdou souhvězdí jako Orion z východu na západ rovně nad hlavou. Bez zatáčky.
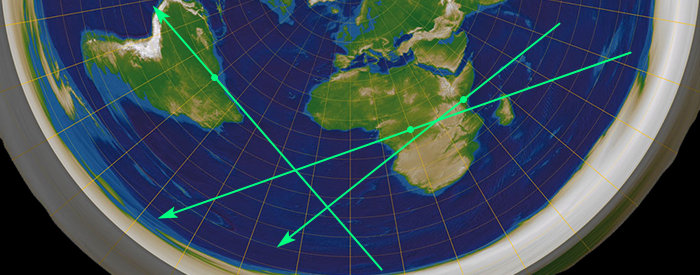
Stejně jako slunce při rovnodennosti, když už jsme u toho. Jdou rovně, jasný? Neuhybaji nikam na sever.
(Na rovníku při rovnodennosti se například stín vidlí zapíchnutejch v zemi bude celej den pohybovat po přímce, což vyvrací pohyb slunce na PZ.)
Tady se můžete podívat jednak na tu rovnou trasu rovníkovejch hvězd, a jednak na to, jak se ty trasy na každej polokouli točí na opačnou stranu. Tohle krátký video vůbec celkem srozumitelně ukazuje, že Země je kulatá a točí se. Na PZ by tohle nešlo.
(Kdo nemá místo mozku lívanec, může se taky zamyslet nad tim, že na zeměkouli všechny tyhle pohyby v rozmezí 24 hodin vysvětluje jen samotný točení Země a nic víc neni třeba – a všechno přesně vychází – zatímco na PZ je Země statická a každej z těch biliónů objektů na obloze se musí nějak hejbat vlastní silou, každej po jinej vlastní komplikovanej trajektorii, a všechno to musí něco pohánět. A nevychází to ani tak.)
Odpovědi na otázky lívanců
Lívanci maji spoustu otázek typu “jak to, že na kouli…” nebo “jak je na kouli možný, že…”.
Primární odpověď je: Jestli vás to opravdu zajímá, proč jste si to ještě pořád nezjistili??
Je zvláštní, že se na to ptaji náhodnejch lidí, místo aby si to prostě našli na Internetu (nebo nedej bože v knížce). Model kulatý Země neni žádná obskurní teorie, která by nebyla dostatečně vysvětlená. Během pár minut se daji ty odpovědi snadno zjistit. No ale že jsem dobrák od kosti, tak na pár z nich odpovim, když už mi je nějakej ten lívanec položil.
Aspoň bude vidět, na jaký nesmysly se lívanci ptaji, jak jednoduchý věci si nedokážou sami zjistit, a jak málo toho chápou o tématu, který je údajně zajímá.
Proč necítíme pohyb Země?
Neni žádnej důvod, proč bysme měli. Jak jsem vysvětlil v PZ1, pohyby Země jsou konstantní, a tudíž neni důvod je cítit. Rotace má konstantní rychlost, oběh kolem slunce taky, gravitace je konstantní síla… nic z toho se nemění.
To, co “cítíme”, jsou “změny” v pohybu, a to zejména změna směru a změna rychlosti, neboli zrychlení a zpomalení. To si lze lehko ověřit v autě nebo výtahu, kde ztrácíte stabilitu jen při změně rychlosti (rozjezd/brzda) nebo směru (v autě).
Při konstantní rychlosti, přímym směru a dokonale rovnej silnici v autě žádnej “pohyb” necítíte. Jakejkoliv pohyb, kterej v autě cítíte, je důsledkem zatáčení, zrychlování, nebo nerovností silnice. Země nikam nezrychluje, nemění dráhu, a pohybuje se vakuem, který se obecně vyznačuje absencí hrbolů. Neni žádnej důvod očekávat, že něco z toho budete “cítit”.
Tahle lívancová otázka má spoustu hloupejch podotázek. Rádi se ohání tim, že na Zemi rotujeme “šílenou” rychlostí 1670 km/h a že to bysme museli cejtit. To je zase něco, co si poslechli na youtube a nechápou, co to číslo znamená a k čemu se vztahuje (a hlavně k čemu se nevztahuje).
V první řadě, Země rotuje rychlostí 1 otáčka za 24 hodin. To je 0.00001 otáčky za vteřinu. Rychlost jak prase. Málem z toho zvracim. Co s těma 1670 km/h? Pokud se vážně chce někdo ohánět tim, že se “pohybujeme” touhle rychlostí, tak je nutná otázka, “vzhledem k čemu?”
Odpověď je, že se pohybujeme rychlostí 1670 km/h (Mimochodem jen na rovníku – v ČR je to 1073 km/h a na pólu je to nula. Proč se čeští lívanci ohání rychlostí ~1670 km/h? Protože si to poslechli na youtube a nikdy si to sami nespočítali, ani o tom nepřemejšleli a neví, odkud se to číslo vzalo.) po kruhu vzhledem k ose Země. K čemuž se dá rozumně dodat snad jen, “No a co?” Jak je pro nás tady na povrchu relevantní naše “rychlost z pohledu osy Země”? Neni.
Podobnej nesmysl je ohánět se tim, že letíme kolem slunce “rychlostí 107 000 km/h”. Vůči čemu? Vůči slunci. Opět: no a co? Jak je pro naši stabilitu na Zemi relevantní pozorování ze slunce? Nijak. A pak samozřejmě lívanci poukážou na to, že celá sluneční soustava obíhá kolem středu galaxie a z toho už by se nám fakt měla motat hlava. Mně se teda motá. Ale jen z hlouposti lívanců.
Stojíme na povrchu Země a vůči němu se nehejbeme.
Pro spoustu lidí jsou tohle možná nejasný abstraktní koncepty, ale můžeme si je snadno objasnit příklady ze světa, kterej dobře známe. Když stojíte v jedoucím vlaku a vyskočíte kolmo nahoru, kam dopadnete? Dopadnete někde jinde, protože vlak, jedoucí 50 km/h, vám za dobu vašeho skoku “ujel” o 10 metrů? Ne. Dopadnete na stejnym místě, ze kterýho jste vyskočili. Tohle víme ze zkušenosti.
Stejně tak, když vyskočíte kolmo vzhůru na Zemi, nedopadnete o 200 metrů vedle, protože se Země o takovej kus mezitim otočila. Jste součástí toho prostředí. Pokud se povrch Země pohybuje rychlostí 1670 km/h (budeme na chvilku předstírat, že pohyb vůči zemskej ose je pro nás relevantní a ignorovat, jestli jsme na rovníku nebo někde jinde), tak se ale stejnou “rychlostí” pohybujete i vy, když na ní stojíte, a když vyskočíte, máte setrvačnost tý “rychlosti Země” – když se na to teda někdo chce dívat z tohodle (upřímně řečeno dost hloupýho) pohledu.
Stejně tak v tom vlaku jste z hlediska fyziky součástí prostředí toho vlaku. Pokud jste zvládli základní školu, tak vás to tam učili pod pojmem “inerciální vztažná soustava”. Jste součástí týhle soustavy toho vlaku (nebo tý Země). Pokud je vaše prostředí (i s váma) v “konstantním” pohybu (vůči něčemu totálně irelevantnímu), z vašeho pohledu je v klidu.
Tohle je vážně důležitý, takže si to zopakujeme: Pokud je prostředí přímo kolem vás v konstantnímpohybu, z vašeho pohledu je v klidu. To, že neni v klidu “z pohledu zemský osy”, je vám úplně stejně ukradený, jako to, že vlak neni v klidu “z pohledy stromu u kolejí”. Strom u kolejí neni součástí inerciální vztažný soustavy vlaku; vy jo.
A stejně jako to, že se oproti tomu stromu pohybujete rychlostí 50 km/h, vám nijak nebere stabilitu v tom vlaku, tak to, že se pohybujete rychlostí 1670 km/h oproti zemskej ose, vám nijak nebere stabilitu na Zemi. A je úplně jedno, jestli ten vlak jede 5 km/h, 55 km/h, nebo 155 km/h. Pokud je ta rychlost konstantní, jste v něm pořád stejně stabilní (pokud vlak nezatáčí a ignorujeme možný nerovnosti kolejí).
Je teda jasný, že úplně stejně irelevantní je rychlost oběhu Země kolem slunce, protože pokud je konstantní, tak na vaši stabilitu na povrchu Země nemá žádnej dopad. A zatímco koleje a silnice můžou mít nějaký hrboly, cesta kolem slunce žádný nemá, stejně jako rotace Země. Neni tu co cítit.
Když jste v dopravním letadle, který 10 km nad zemí letí rychlostí 1000 km/h, můžete mi říct, jak “cítíte” jeho rychlost? Vážně, může mi někdo popsat, jak tuhle hroznou rychlost cítí? Já tam nic takovýho necítil a dalo se tam v pohodě spát. Možná jsem jen natvrdlej. Co jsem měl cítit? 1000 km/h je rychlý, ne?
Pokud by se nějakej superchytrák chtěl zeptat, proč z tý koule neodletíme “odstředivou silou” v důsledku její rotace, tak v první řadě rotace 0.00001 ot/s fakt žádnou velkou odstředivou sílu negeneruje, a za druhý gravitace, která působí opačnym směrem, je mnohem silnější.
To, že lívanci nechápou nic o gravitaci, na tom nic nemění. Gravitace a odstředivá síla jsou dvě síly opačnýho směru. Výsledná síla, která na vás působí, bude teda rozdíl těch dvou sil, ve směru tý, která je z těch dvou větší. Pokud má gravitace sílu “10” a odstředivá síla “1”, bude na vás působit síla s hodnotou “9” ve směru gravitace. Neni to nijak složitý.
Lívanci poukazujou na šílenou trajektorii člověka na Zemi, která se točí kolem osy, obíhá kolem slunce, obíhá kolem středu galaxie, atd., a maji strašně rádi tu počítačovou grafiku, která se objevuje v každym youtube videu lívanců a ukazuje to jako takovou hrozně chaotickou spirálu. Tohle na ně evidentně dělá velkej dojem, protože vůbec nemaji tušení, co to znamená v reálnym světě.
Můžeme si ten příklad s vlakem teda ještě prohloubit, pro lepší pochopení komplexních pohybů. Ve vlaku si například můžete házet tenisákem o zeď a podlahu, a půjde vám to celkem stejně, jako v normálním pokoji. Z pohledu stromu venku má ten tenisák dost chaotickou trajektorii. Jenže tomu tenisáku je pohled stromu úplně u prdele a z vašeho pohledu se odráží úplně normálně, jako v místnosti.
Zkomplikujeme to ještě víc. Představte si velkej nákladní vlak, kde se na jeden vagón naloží kulatá otočná místnost bez oken, ve kterej budete sedět. Řekněme, že máme super technologii, takže je to vlak maglev bez drncání, místnost má perfektní mechanismus, takže se točí velmi plynule, a prostě všechno je dokonalý.
Vlak jede 200 km/h po dlouhej rovnej magnetickej trati. Místnost se otáčí rychlostí třeba jedna otáčka za 5 minut. Nemá žádný okna a má dokonalou zvukovou izolaci. Takže sedíte na vlaku, kterej jede 200 km/h, v místnosti, která se točí rychlostí 0.003 otáčky za vteřinu, neboli asi 300x rychlejc než Země. Nevidíte ven a neslyšíte zvenku zvuk.
Ucejtíte nějakej “pohyb”? Neucejtíte. Padáte ze židle? Nepadáte. Teď si na jednej straně místnosti postavíme stoleček, a na něj dáme otočnej tác na motůrek se zákuskama a na něj zákusky. Tác se točí rychlostí 1 otáčka za minutu. Takže chudák zákusek se točí rychlostí 0.016 ot/s (asi 1500x rychlejc než Země) na tácu, u stěny místnosti, která se točí rychlostí 0.003 ot/s, ve vlaku, kterej jede 200 km/h.
Podle lívanců by ten zákusek měl z toho tácu lítat na všechny strany a bejt totálně zmatenej (stejně jako jsou oni) z tý naprosto chaotický trajektorie a šílený rychlosti všech těch pohybů (z pohledu stromu u kolejí). Jenže nic takovýho se neděje, protože zákusek je součástí inerciální vztažný soustavy toho tácu a je úplně v klidu.
Chaotická trajektorie z pohledu stromu u kolejí je pro něj naprosto irelevantní, stejně jako je pro nás irelevantní “pohled” ze středu galaxie. Jsme tady na povrchu Země. Pohybujeme se “s nim” (pokud se teda na to, že stojíme na Zemi, mermomocí chcete dívat jako na “pohyb”, což je celkem blbost).
Ten zákusek je na tom ve skutečnosti hůř než my, protože obě točení nemaji vlastní gravitaci (do středu točení), která by vyvažovala odstředivou sílu, a všechno je zároveň v gravitačním poli Země, což věci komplikuje, zatímco pro nás se odstředivá síla a gravitace vyvažujou jak v případě otáčení, tak v případě oběhu. Při danejch rychlostech ale vidíme, že zákusek, podléhající třem úplně odlišnejm pohybům, bude i tak v klidu sedět na tácu. (Akorát když vedle zákusku položíte lívanec, bude tomu zákusku tvrdit, že se s nima nic netočí a žádnej vlak neexistuje.)
Chápeme? Neni to nic abstraktního a teoretickýho. Vidíme v reálnym světě, jak to funguje. To, že několik různejch konstantních pohybů s váma nedělá žádný psí kusy, si můžete snadno vyzkoušet v praxi. Takže ty bláboly o “1670 km/h”, který se lívanci naučili z youtube, by měli radši dát stranou, protože se tim jen ztrapňujou.
Jak může na kulatej Zemi fungovat sextant?
To je mi zase ignorantská otázka. Při práci se sextantem, jak se dočtete kdekoliv, kde se o práci se sextantem píše, se používaji tabulky pro korekci pro zakřivení Země. Klíčový slovo používaji. Konkrétně se bere v úvahu nadmořská vejška pozorovatele, z níž se vypočítá rozdíl mezi zdánlivym horizontem a skutečnym horizontem, kterej vzniká v důsledku zakřivení Země.
Jelikož tuhle korekci všichni, kdo pracujou se sextantem, aplikujou, neboli používaji sextant s vědomím, že Země je kulatá, tak tu otázku jen obrátim: Jestli je Země plochá, tak proč se při práci se sextantem dělaji korekce pro zakřivení Země? Nemělo by pak všechno vycházet špatně?
Evidentně lívanci, kteří se na tohle ptaji, se ani jednou nepokusili si o tom něco přečíst. Je to zase něco, co slyšeli na youtube, papouškujou to, a nic o tom neví. A sextant neni jediná věc, která se používá s předpokladem, že Země je kulatá (a funguje), a kdyby Země byla plochá, dávalo by to jiný výsledky.
Jak to, že je na kouli odraz na hladině po celej dýlce od horizontu až k pozorovateli?
Tahle otázka naráží na tohle:

Podle lívanců, kterejm to moc nemyslí, by ten odraz “neměl jít po celej dýlce, protože zeměkoule má bejt zakřivená”. Ach bože. -_-;
Takže se pokusíme zapojit aspoň dvě procenta svojí mozkový kapacity a jdeme na to.
Jednoduchej fakt, kterej by si měl uvědomit každej, kdo neni totální tupoň, a rozhodně každej, kdo se jako hrdej lívanec pyšní tim, že o věcech přemejšlí víc než ostatní lidi, je to, že na moři jsou vlny. A na vlně se vždycky najde nějaká část, která to světlo odrazí přímo na vás. Fakt hrozná věda.
Máme tu tři obrázky. Proč myslíte, že ten odraz na tom prvním je takovej rozblemcanej a přerušovanej? Protože vlny. Na tom třetím vidíte, jak v tej přední části je ten odraz úplně rozhozenej, protože jsou tam jiný vlny. A na tom prostředním vidíte nádherně kromě těch všudypřítomnejch malejch vlnek ještě ty větší, na kterejch je dokonale demonstrováno, co dělaji vlny s odrazem světla. Z každý se někde odrazí.
Že lidi, kteří si o sobě myslí, že jsou inteligentní, nedokážou na tohle přijít sami, mi připadá tragický.
Tady pohled zblízka, pro lepší představu:

Ve skutečnosti jsou to miliardy jednotlivejch odrazů. Kromě toho tu opět hraje roli (lívancům naprosto nepochopitelná) atmosférická refrakce.
“No ale počkej, Antivire, a co na klidnym jezeře bez vln? Tam by to teda nemělo bejt po celej dýlce, ne?” No já nevim, tak se teda asi zkusíme na nějaký podívat, jestli nikdo nemá lepší nápad…

No do prkenný vohrady! Zatracená realita! Proč s těma lívancema vůbec nechce spolupracovat?
Mimochodem, vy lívancoví géniové, když jste přišli na to, že na kulatej Zemi by ten odraz neměl bejt po celej dýlce, tak proč jste nepřišli na to, že na plochej taky ne??
[Navrhuju minutu dramatickýho ticha a pořádně se zamyslet. Pak si můžete cvičně nafackovat.]
Bohužel takhle “kvalitní” je většina argumentů a otázek lívanců.
Tady máme tu refrakci:

Jsou tu “nelogicky” dva odrazy. Jeden “normální” a druhej v zóně, kde je efekt atm. refrakce silnej. Z toho si můžete dovodit, že tenhle efekt ten odraz někdy dokáže “prodloužit”. V tomhle případě byl ten efekt takovej, že to dokonce rozdělil na dvě části.
Proč vidíme celej rok stejný hvězdy?
Těžko říct. Možná proto, že místo na oblohu koukáte na obrázek? Nebo na americký filmy? Tam se ty Hollywoodský hvězdy v průběhu roku moc nemění. Na obloze ale v zimě vidíme jiný souhvězdí než v létě, takže tahle otázka je dalším důkazem, že papouškujete otázky z youtube videí a nevíte, o čem mluvíte. Na noční hvězdnou oblohu jste se ve skutečnosti evidentně nikdy nedívali.
Jak to, že nevidíme, že se budovy na obzoru naklání pryč od nás?
Že by to bylo proto, že patříte k rase Homo Lívanec a ne k rase Superman? Na 50 kilometrů (což už je zatraceně daleko, viz Chicago) to dělá míň než půl stupně. Jak chcete sakra vidět sklon půl stupně směrem od vás na 50 km?? Zkusili jste se nad tim aspoň na 5 vteřin zamyslet?
Proč má měsíc jinou teplotu světla než slunce, jehož světlo údajně odráží?
Blábol. Světlo nemá “teplotu” (pokud se teda nebavíme o zabarvení světla, ale to lívanci nemyslí).
Lívanci tvrdí, že objekty, na který v noci svítí měsíc, maji nižší teplotu než objekty ve stínu. To se sice tak trochu děje, ale samozřejmě to neni efekt světla měsíce, protože to je kravina (světlo vám vážně nemůže nic “zchladit”), ale souvisí to s vyzařováním tepla danýho objektu.
Objekty “ve stínu” toho tepla vyzařujou míň (a tudíž jim ho víc zůstává), protože je něco “blokuje” (to, co na ně háže ten stín). Je to ten důvod, proč je za jasný noci větší zima než když je zataženo. Mraky (částečně) blokujou vyzařování tepla ze země. Takže to s měsícem nemá nic společnýho, což si můžete ověřit tim, že ten efekt je stejnej i v noci, kdy měsíc nesvítí.
Na detailní vysvětlování je to trochu složitý, takže koho to zajímá víc, ať se podívá na tenhle docela detailní experiment, kde to chlápek podrobně rozebírá a měří za různejch podmínek, s měsícem i bez něj. (I když neumíte anglicky, tak to pochopíte a uvidíte výsledky měření. Prvních pár minut povídání můžete přeskočit.) Hlavní pointa je, že ten rozdíl teplot nemá nic společnýho s měsícem a představa, že měsíční světlo “chladí”, je jen další blábol negramotnejch pomatenců.
Jako bonus chlápek ve videu taky ukazuje příklad, na kterym je vidět, že slunce neni lokální, protože osvícení měsíce a koule na zemi má úplně stejnej úhel:

Což je docela pěkný. Na PZ by na měsíc světlo ze slunce mělo dopadat vodorovně a na tu kouli na zemi shora. Což se samozřejmě neděje a na oba objekty dopadá zhruba ze stejnýho úhlu. (Protože je hóóódně daleko.)
K tématu měsíčního světla a teplot jsem našel i tuhle pěknou vědeckou studii. Nevim, jestli jsou lívanci obeznámeni s fenoménem vědeckejch studií, protože oni sami žádnou nikdy nevyplodili. Je to takovej způsob, jak objektivně otestovat, jestli je něco pravda nebo neni. Takže autor týhle studie testoval, jestli věci v měsíčním světle maji nižší teplotu než ve stínu.
V úvodu vysvětluje, že je mnoho způsobů, jak se špatně navrženym experimentem (ať už omylem nebo záměrně) dá dosáhnout celkem jakejchkoliv výsledků. Jak už jsem říkal, země pod čistym nebem vyzařuje víc tepla než země pod mraky, střechnou, stromy, a podobně, takže bude ukazovat nižší teplotu, bez ohledu na měsíc. Autor studie zároveň poukazuje na to, že vodorovný plochy budou vyzařovat jinak než svislý, že záleží na tom, jak na daný místo svítilo slunce v průběhu dne, že různě vyzařujou teplo různý materiály, atd.
Takže se dá lehko dosáhnout klamnýho zdání, že místo v měsíčním světle je chadnější než místo ve stínu. Neni to ale měsícem, nýbrž jinejma faktorama (což bylo demonstrováno i v experimentu v tom videu). Takže je třeba v první řadě srovnávat dvě místa, který maji stejný vlastnosti.
Autor studie proved řadu experimentů, kde srovnával místa v měsíčním světle a ve stínu pod čistym nebem, stejně jako obojí pod stromem, plus další kontrolní testy, a všechno měřil opakovaně mnohokrát za sebou a pak to průměroval.
Výsledek byl jednoznačnej. Místa v měsíčním světle nejsou chladnější než místa ve stínu, a zároveň místa pod čirym nebem jsou chladnější než místa pod nějakym krytem. Je ale extrémně snadný natočit video, kde to bude vypadat, že teploty ve stínu jsou vyšší než v měsíčním světle. Lívanci tomu pak uvěří jako “faktu”, a opět to všude šíří, aniž by cokoliv chápali o tom, co se ve skutečnosti děje.
Možná se teď ptáte, co má tahle kravina vůbec společnýho s tvarem Země. Nic. To jen, že lívanci nevěří, že měsíc odráží sluneční světlo. Myslí si, že má vlastní. (Netušim, proč potom “svítí” vždy jen ta strana, na kterou svítí slunce, ale to už je jak řešit bradavice u někoho, kdo má AIDS, pokročilou metastázu rakoviny, vypíchnutý oči a zlámaný obě nohy a ruce.) Jednak to ale zase ukazuje mimóznost lívanců, a jednak se na to dá snadno odpovědět, tak jsem to sem zahrnul. Ať si z toho každej vyvodí vlastní závěry.
Proč nemusí letadla korigovat let natočením “čumáku” dolů, aby letěly v konstantní vejšce?
Další vtipná otázka, kterou se lívanci naučili na youtube a papouškujou ji, aniž by chápali cokoliv o lítání letadel a o atmosféře. Tady si zase myslí, že když letadlo poletí “rovně”, tak by mělo uletět ze Země pryč. To je samozřejmě totální blbost. Letadlo nemůže uletět do vesmíru, ani kdyby chtělo.
O pilotování letadel sám taky nic nevim, ale když tomu nerozumim, tak si to buď nastuduju, nebo necpu lidem ignorantský nesmysly. Když už se ke mně ta otázka dostala, tak jsem si řek, že by nebylo špatný vědět trochu víc o tom, jak to s těma letadlama a udržováním vejšky funguje. A protože jsem (mnohem!) chytřejší než lívanci, tak jsem udělal takovou hrozně fikanou věc, která by je nikdy nenapadla: zeptal jsem se pilota.
Lívanec se pilota nezeptá, protože typickej lívanec nechce znát odpovědi na tyhle otázky (protože by mu to vyvracelo jeho víru). Lívanec chce házet tyhle blbý otázky po melounech, a doufá, že narazí na dostatečně hloupýho melouna, kterej se těma jeho kravinama nechá oblbnout, a obrátí ho na víru ve velkej lívanec.
Letadlo nemůže uletět někam pryč ze Země, protože nad určitou vejšku se prostě nedostane. Důvodem je, že už je tam moc řídkej vzduch. Podobně jako vy můžete máváním rukama plavat ve vodě, ale ve vzduchu ne, protože je moc řídkej, vrtule letadla potřebujou nějakej odpor vzduchu, aby ho to pohánělo. Když je moc řídkej, nejde to.
Takže letadlo má nějakou maximální vejšku, přes kterou se nedostane. Znamená to, že teda letí v tej maximální vejšce? Neznamená. Když letadlo letí rovně, nahoru ho posouvá vztlak křídel a dolu gravitace. Když se zvýší výkon motoru, zvýší se rychlost vpřed a tim i vztlak – letadlo stoupá. Když se výkon sníží a letadlo zpomalí, gravitace převládne nad vztlakem a letadlo klesá.
Stoupá nebo klesá takhle do nekonečna? Ne. Vzduch je nejhustší u země a směrem nahoru postupně řídne. Hustota vzduchu je to, co to letadlo udržuje v konstantní vejšce. Když přidáte plyn, letadlo bude stoupat, ale jen to tý doby, než se dostane do tak řídkýho vzduchu, že mu to už další stoupání nedovolí. Na tejhle úrovni se bude držet.
Neboli při konstantním výkonu motorů se bude letadlo držet v konstantní vejšce. Když ho nějaká turbulence hodí vejš, motory hrabou do řidšího vzduchu a v něm nemaji takovou “sílu” a letadlo zas klesne na původní vejšku. Když ho turbulence hodí níž, motory v hustším vzduchu zaberou víc a vztlak letadlo vrátí do původní vejšky.

Takže jelikož se konkrétní vejška nad zemí (nebo spíš mořem) vyznačuje specifickou hustotou vzduchu, letadlo se v ní automaticky drží, protože se drží v určitej zóně hustoty vzduchu. Natáčení čumáku nahoru nebo dolu v tom ani nehraje žádnou roli.
Natáčení čumáku pomáhá, když chce pilot změnit vejšku hodně, takže to se používá hlavně při vzletu. Při klesání se prostě sníží výkon a nechá se to pomalu klouzat dolu. Neni důvod se k tej zemi hnát jak o závod. Pro udržení konstantní vejšky neni třeba nic dělat s čumákem letadla.
Tohle by samozřejmě lívanci zjistili, kdyby se o to pokoušeli. Jak jsem ale už dobře pochopil, oni ve skutečnosti nechtěji nic vysvětlit. Chtěji obracet melouny na lívancovou víru. Mě nemaji rádi, protože já jim ty jejich blbosti snadno vyvracim a konfrontuju je s realitou, kterou nechtěji vidět. (A samozřejmě je ještě zesměšňuju. Jenže jak je nemám zesměšňovat, když melou takový hovadiny? Víte, jak je to těžký?)
Blbosti, výmysly a lži lívanců
“Neexistuje žádnej důkaz zakřivení Země”
Zbožný přání lívanců. Důkazů je spousta, jak jsme tady viděli. Lívanci je většinou ani nevyvrací, ale jen ignorujou a odvádí pozornost někam jinam. Třeba začnou blábolit o gyroskopu nebo tak něco.
“Nikde neni vidět zakřivení horizontu zleva doprava”
Tady je nutno poznamenat, že hodně, možná i většina, lívanců ví, že tohle je blbost. Ale pořád se najde spousta těch, kteří si myslí, že by na moři mělo bejt vidět zakřivení zleva doprava, a absenci takovýho zakřivení berou jako důkaz plochosti Země. Nic takovýho samozřejmě bejt vidět nemůže.
Když budete na moři na člunu a neuvidíte žádnou pevninu, tj. v celym kruhu 360° kolem vás bude vodní obzor, jak by se asi tak měl křivit? Když budete koukat jednim směrem a obzor by se zakřivoval zleva doprava, tak co by se mělo stát, když se otočíte doprava? Kam ten obzor bude pokračovat?
Každej bod na tom obzoru je ve stejnej vejšce (vzdálenost od středu Země), která je zhruba stejná jako vaše vejška. Koukáte se na kruh z prostředka toho kruhu. Takhle se jeho zakřivení vidět nedá.
Můžete si to vyzkoušet třeba s obručí na cvičení, nebo nějakym podobnym kruhem o průměru kolem metru. Držte ten kruh vodorovně kolem svojí hlavy ve vejšce očí. Vidíte jeho zakřivení? Pokud je ve vejšce vašich očí, tak samozřejmě ne.
Když jste na moři, tak jste nad úrovní toho “kruhu” na obzoru o tak málo, že je to jako s tou obručí, kdyby se úroveň vašich očí zvedla o milimetr. Pořád žádný zakřivení neuvidíte. Až z výrazně větší vejšky – když už se na ten kruh díváte zřetelně shora – uvidíte to zakřivení. Na Zemi to chce desítky kilometrů. Z úrovně země se takhle její zakřivení vidět nedá.
Ze stejnýho důvodu neni vidět, že se budovy na dvou místech na horizontu “naklání pryč od sebe”. Zase kravina z youtube, která nedává žádnej smysl.
“Slunce mizí do dálky”
Evidentní blbost. Slunce má z našeho pohledu pořád stejnou velikost, což je dost dobrá známka toho, že je pořád stejně daleko. Věci, který “mizí do dálky”, se zmenšujou (jak ví každej kromě lívanců), což slunce nikdy nedělá.
“Slunce se přibližuje až úplně k horizontu”
To je nesmysl, kterym se lívanci pokouší nějak okecat to, že západ slunce jejich teorii vyvrací. Něco ve vejšce 5500 km se se vzdalováním sice bude opticky “přibližovat k horizontu”, ale nikdy se ho nemůže dotknout, natož klesnout pod něj, což už je naprosto evidentní hovadina. Mezi tim horizontem a tim sluncem je vždycky těch 5500 km.
Tvrzení, že věci mizící do dálky se přiblíží až k horizontu, zároveň vyvrací třeba to, že letadla to nedělaji. Běžně nám mizí z dohledu vysoko ve vzduchu. (Před čímž se hajzlíci záludně zmenšujou.)
A můžete se zamyslet nad jednoduchou věcí: Průměr slunce je podle lívanců 51 km. Jeho vzdálenost od Země je 5500 km. Takže jednoduchej fakt: Bez ohledu na to, jak blízko se slunce k horizontu opticky přiblíží, vzdálenost mezi sluncem a zemí musí vždycky bejt víc než 100x větší než průměr slunce. S tim, jak se opticky zmenšuje vzdálenost k obzoru, se musí úměrně zmenšovat i průměr slunce!

Jaký přírodní zákony má PZ? Žádný. Všechno pohání zeměplošská magie.
(Ještě se mi někdo diví, že lívance urážim? Jak si mám myslet, že někdo, kdo věří, že na tomhle obrázku slunce “mizí do dálky” a je ve skutečnosti 5500 km nad Zemí, neni úplnej mimoň?)
“Horizont je vždycky ve vejšce očí”
Neni a nemůže bejt, ať je Země kulatá nebo plochá. I na PZ je horizont na úrovni vašich nohou, neboť je to ta země, na kterej stojíte. Když je na úrovni vašich nohou, logicky nemůže bejt zároveň na úrovni vašich očí, pokud teda nejste mutanti s očima na palcích u nohou.
Je to další argument, u kterýho si lívanci neuvědomili, stejně jako u toho s odrazem slunce na moři, že ten jejich domnělej “problém” existuje na ploše stejně jako na kouli.
“Dohled oka neni nekonečnej”
Zajímalo by mě, na čem lívanci tuhle blbost zakládaji. Pokud víme, dohled oka prakticky nekonečnej je. My melouni vidíme hvězdy spoustu světelnejch let daleko. (Lívanci samozřejmě taky, ale nevěří tomu.) To, že na určitou vzdálenost určitý věci nevidíme, je otázka rozlišení a ne dohledu.
Jasně že když je něco moc daleko a moc malý, tak už to nevidíme. To ale neni proto, že tak daleko “oko nedohlídne”. Když v tej samej vzdálenosti bude něco stokrát většího, tak to uvidíme. S “dohledem” tu žádnej problém neni.
Jednoduchej příklad: Když koukáte na budovu 5 km daleko a kolem ní letí sýkorka, sýkorku nevidíte. Neni to proto, že tak daleko vaše oko nedohlídne, ale proto, že na tu vzdálenost je pro rozlišení vašeho oka moc malá. Budovu na tu samou vzdálenost vidíte. Jasný?
Když připustíme, že lívanci maji hvězdy “blízko” a nic neni světelný roky daleko, tak můžeme teoreticky spekulovat o tom, že by oko mělo nějakej “maximální dohled”. Problém je v tom, že jak jsme viděli, měsíc je vidět třeba na vzdálenost 20 tisíc km, hory jsou vidět na několik stovek kilometrů, ale lívanci používaji tenhle argument k vysvětlení toho, že na moři nevidíme jeho břeh už třeba z 20 km, ani s dalekohledem. To je naprosto nelogický. (Jak jsme viděli, foťáky máme dost dobrý na vidění věží Chicaga na 85 km.)
Jednoduchá otázka pro lívance: Jakej je dohled lidskýho oka?
Na tohle žádnej lívanec neodpoví, protože by byl okamžitě usvědčenej ze lži.
“Světlo se na plochej zemi láme tak, že země/voda zakrejvá vzdálený objekty”
Jelikož na moři běžně vidíme, že nám obzor zakrejvá spodní část měst, lodí, a podobně, někteří lívanci si vymysleli, že světlo se láme tak, že voda mezi váma a pozorovanym objektem na obzoru zakrejvá jeho spodní část. Pro tohle tvrzení ale neexistuje žádnej vědeckej podklad.
Pomineme, že atmosférická refrakce má ve skutečnosti úplně opačnej efekt – je vidět dál za horizont. Na placce by ten efekt nebyl. Čim je ale odůvodněný tvrzení, že se světlo láme tak, že voda 5 km od vás zakrejvá půl lodi 10 km od vás? Ničim.
Světlo se tak teoreticky, za určitejch okolností, lámat může. V důsledku rozdílnejch teplot a tlaku na různejch místech se světlo může lámat všelijak. Tenhle způsob lámání světla ale neni nijak běžnej a už vůbec ne všudypřítomnej. Zakrejvání spodní čísti objektů obzorem ale je obecnej jev, kterej pozorujeme všude, kde se nám na moři něco dostatečně vzdálí. (Jako na těch 20+ fotkách Chicaga tady.)
Je dobrý si uvědomit, že aby tenhle efekt nastal, tak něco, co je dole, musí bejt vidět vejš než něco, co je nahoře. Voda před lodí je z vašeho pohledu logicky níž než jakákoliv část tý lodi. Tvrdit, že se světlo normálně láme tak, že tu vodu vidíme vejš než spodek lodi, je hloupej nesmysl.
Tenhle argument si lívanci jen vymysleli, aby se vykecali ze svejch lží. Až vám nějakej lívanec bude tuhle blbost vnucovat, chtějte po něm vysvětlení, proč se to světlo všude láme zrovna takhle. Taky by mohli poskytnout nějakej zdroj pro tohle tvrzení. (Zdroj, kterej neni “video lívance na youtube”.)
“Když víc zazoomuješ na loď zpola zakrytou obzorem, ukáže se celá”
Další zoufalej blábol, kterej se nedá podložit žádnejma faktama a je očividně nesmyslnej. Je to opravdu jednoduchý: Zoomování zvětšuje, nemění úhel pohledu. (Kromě na CSI, tak nevim, jestli lívanci moc čumí na americký seriály.) Tohle by měl chápat každej, kdo strávil nějakou dobu v 21. století při vědomí.
Samozřejmě si to kdokoliv může ověřit. Představa, že když zazoomujeme na loď, jejíž spodní polovinu zakrejvá obzor, tak ji uvidíme celou, je stejně pomatená jako představa, že když zazoomujeme na auto, jehož polovinu nám zakrejvá roh budovy, tak ho uvidíme celý.
Zoomování na loď nebo město na obzoru, jehož spodní polovinu zakrejvá obzor, vám nemůže ukázat celou loď/město, stejně jako zoomováním nemůžete vidět za roh. Proč se něco takovýho v 21. století musí vysvětlovat dospělejm lidem, mi neni moc jasný.
(Mimochodem tenhle blábol je v rozporu s tim předchozím. Buď ta voda zakrejvá půl lodi kvůli lámání světla, nebo kvůli zoomu. Tak si vyberte. Obojí jsou ale stoprocentní hovadiny.)
“Vodní hladina je vždycky rovná, takže oceán na kouli nemůže fungovat”
Lívanci si pletou pojmy a maji potíže chápat, jak funguje gravitace. Vodní hladina neni “plochá”, ale “vodorovná”, což jsou dva odlišný pojmy. Plochost je, když všechny body na hladině jsou v jednej rovině. Vodorovnost je, když všechny body na hladině jsou stejně daleko od centra gravitace.
Všechno na Zemi je přitahovaný k centru její hmoty, tj. ke středu Země. Možná nikdo neví, proč přesně se to děje, ale víme, že se to děje. Hladina oceánu teda neni “plochá”, ale “vodorovná”, což na Zemi znamená zakřivená. 
Mimochodem, tvrzení, že hladina je vždycky rovná, neni pravda ani v malym měřítku. Kapka vody neni rovná. Hladina ve zkumavce neni rovná. Vtipně i ve vodováze máme bublinu ve vodě, která je kulatá. Takže to je zase něco, co lívanci papouškujou z youtube videí a neni to pravda.
Někteří lívanci dokonce melou něco o tom, že “na kouli tečou řeky do kopce”. Zatim mi nikdo nevysvětlil, co přesně timhle absolutním nesmyslem myslí, ale zřejmě to souvisí s jejich nechápáním gravitace. Řeky tečou z větší nadmořský vejšky do menší, respektive z “větší vzdálenosti od středu Země” do “menší vzdálenosti od středu Země”, v důsledku gravitace.
Pokud někdo tvrdí, že řeky tečou “do kopce”, tak ať mi vysvětlí, co tou neskutečnou blbostí vůbec myslí.
Závěry
Země je prokazatelně kulatá
Když si to shrneme, máme několik naprosto jednoznačnejch důkazů, že Země je kulatá, slunce je hodně daleko, a model PZ, pokud se tomu vůbec dá říkat model, je směšná slátanina totálních blbostí.
- Skutečný naměřený vzdálenosti na Zemi odpovídaji kouli a neodpovídaji PZ.
- Skutečný lety letadel jsou konzistentní se vzdálenostma na kouli a na PZ ne.
- Objekty mizí za horizont úměrně s narůstající vzdáleností od nich, a to odspodu.
- Západ slunce je důkazem zakřivení Země a na PZ neni možnej.
- To, kam v kteroukoliv dobu dopadá sluneční světlo, jasně dokazuje, že Země je kulatá.
Na PZ to neni žádnym způsobem možný reprodukovat.
- Polární den za jižním polárním kruhem je na PZ nemožnej.
- Slunce v modelu PZ je večer až třikrát dál než v poledne, a přitom má stejnou velikost.
To je nemožný a konstantní velikost slunce ukazuje, že je pořád zhruba stejně daleko.
- Vidět vždy jen jednu stranu měsíce je na modelu PZ nemožný. Funguje to jen na kouli.
- Zatmění měsíce je na PZ nemožný.
- Skutečný pozorování jižních souhvězdí se nedá žádnym způsobem napasovat na model PZ.
Je perfektně konzistentní s rotující zeměkoulí.
Zjistit, jakej tvar má Země, nevyžaduje nijak zvláštní speciální vědomosti ani žádný speciální vybavení. Stačí troška základního vzdělání, dívat se na věci, který vidí každej, a trochu přemejšlet. A když říkám “vzdělání”, tak tim myslim “chápání, jak fungujou běžný věci kolem nás“. (Aby si někdo nemyslel, že to má něco společnýho se školou.)
Tohle byly jen ty nejvýznamnější a nejjasnější důkazy, že Země je kulatá a PZ je blbost, a i tak se jich nahromadilo celejch deset. Existuje spousta dalších důkazů a indikací, že Země je kulatá, stejně jako jevů a faktů, který se na PZ nedaji nijak vysvětlit. Nemá cenu je všechny rozebírat. Lívanci nedokážou vysvětlit těch 10 problémů s jejich modelem, který jsem právě popsal. Dokud se jim to nepodaří, nemá smysl brát jejich “teorii” vážně.
Mezi tím nepřeberným množstvím dalších indikací, že model zeměkoule funguje a model PZ ne, jsou třeba vzdušný proudy, který na Zemi vypadaji asi takhle:
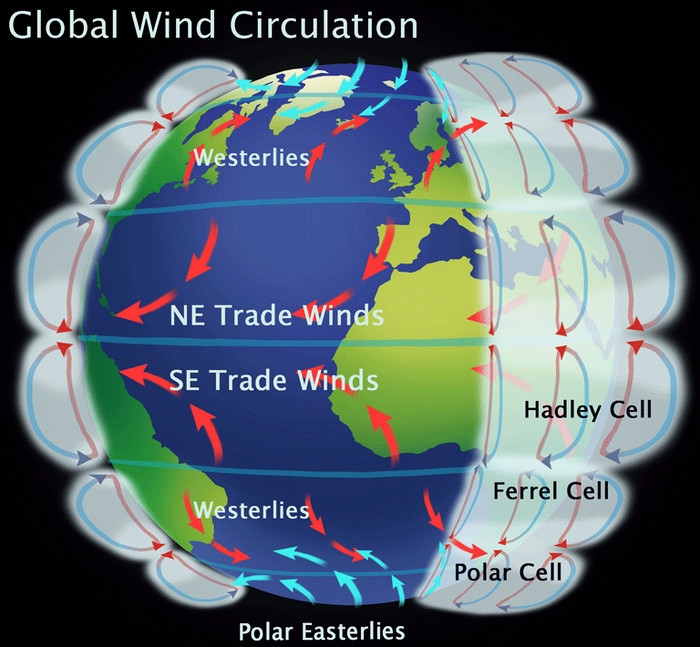
Proč jsou takhle pravidelný a točí se ve zřetelnejch vzorcích? Směr sever-jih je danej rozdílama teplot na rovníku a pólech. Směr východ-západ je danej otáčením Země. Podle lívanců se ale Země nehejbe, takže na PZ tyhle proudy nemá co způsobovat. (A máme tu proudy točící se kolem jižního pólu, kterej na PZ neexistuje, takže stejnej problém, jako s těma hvězdama.)
Kromě toho tu máme problém jižního pólu obecně. Jak funguje na PZ jižní magnetickej pól? Nějaký teorie? Nějaká studie? Aspoň nějaký vysvětlení, kterýmu může uvěřit někdo, kdo neni v hypnóze?
Máme tu i ten fakt, že ve spoustě oborů se musí počítat se zakřivením Země, aby věci fungovaly. Rozsáhlý stavební projekty (v rozsahu kilometrů) musí brát (a berou) v potaz zakřivení Země, aby se daly postavit. Armáda bere v úvahu zakřivení Země při výpočtu trajektorií střel delšího doletu. (Jinak by netrefili cíl, a takový věci bere armáda fakt vážně.) Tohle je ale tak daleko za hranicema vědomostí lívanců (který končí přesně tam, kde končí jejich youtube videa), že vůbec nemá smysl se o tom bavit.
Pak je tu samozřejmě ten problém s gravitací. Poukázal jsem na absurdní model Univerzálního zrychlení, podle nějž Země “zrychluje” směrem nahoru, což vytváří efekt gravitace. Nezodpovězeno zůstává mimo jiné proč ta Země zrychluje, vůči čemu (když podle lívanců neexistuje vesmír), odkud se bere ta energie, proč měsíc a spol. nespadnou na zem, a tak dál.
Jeden lívanec mi napsal, že můj článek je dezinformace a fake news a že o plochej Zemi nic nevim, protože Flat Earth Society jsou podvodníci a jejich modelu Univerzálního zrychlení žádnej lívanec nevěří. Výborně, říkal jsem si, tak se snad dovim něco lepšího. Tak jsem se lívance zeptal, jakej je teda správnej (nebo aspoň jinej) model gravitace na PZ.
Neodpověděl. A tim nemyslim, že už nenapsal. Napsal a napovídal toho dost. Na otázku o gravitaci ale neodpověděl, stejně jako na žádnou jinou moji otázku z toho článku. Pokoušel jsem se najít nějakou jinou teorii gravitace lívanců, ale nenašel. Všechny jejich bláboly na tohle téma končí tim, že “vlastně nikdo neví, co je gravitace, takže…”. Pak rozhodí rukama, jako že žádný vysvětlení nepotřebujou poskytovat, protože nikdo neví, “co” je gravitace.
Nechápou rozdíl mezi modelem či teorií a znalostí, proč ta teorie funguje. Jasně, nevíme, co přesně je gravitace, ale na kouli pro ni máme teorii a model, podle kterýho dokážeme dělat předpovědi, který nám vychází. Máme model, kde gravitace je vlastností těles s ohromnou hmotou, kterou k sobě přitahujou ostatní tělesa. Jelikož v našem blízkym okolí je hodně hmotný těleso akorát Země, gravitace je pro nás primárně síla, která nás táhne směrem ke středu Země.
Bez ohledu na to, proč tahle síla existuje, dokážeme popsat, jak funguje, spočítat ji, a předpovědět, jak velká bude v jakym místě. A v praxi nám to vychází, což je známkou toho, že náš model funguje.
Lívanci kromě Univerzálního zrychlení žádnej model nemaji. Nedokážou gravitaci ani popsat. Ta naše na PZ nemůže fungovat, protože by v první řadě nemohla existovat ani ta placka. Velmi rychle by se zhroutila do hroudy, ze který by se časem stala koule. Lívanci, kteří nevěří na Univerzální zrychlení, nemaji nic. Maji jen tvrzení, že “nikdo neví, co je gravitace”, který je podle nich zřejmě osvobozuje od potřeby myslet.
I v mnoha dalších směrech PZ nemá ani funkční model. Neexistuje žádnej model PZ, kterej by dokázal předpovědět, kde bude kdy vidět světlo slunce a kde ne. Tohle lívanci dokážou předpovědět jen na základě modelu zeměkoule. Na zeměploše se nic takovýho nedá vypočítat.
Lívanci nedokážou sestavit model PZ, v jakymkoliv měřítku, kterej by fungoval. My dokážeme vyrobit fyzickej model Země a slunce a ukázat jejich interakci a kam dopadá světlo, a ten model odpovídá realitě. Lívanci nic takovýho nedokážou. Nebude jim tam vycházet světlo, nedokážou demonstrovat, že odněkud slunce “nebude vidět”, nedokážou demonstrovat, že vzdálenosti na tom modelu odpovídaji reálnejm vzdálenostem, nedokážou na něm ukázat polární den na jihu, nedokážou na něm ukázat zatmění měsíce… prostě nic.
PZ neni “model”. Je to výmysl. Je to nevědeckej paskvil založenej na nesmyslnej víře. Ať zkusí lívanci postavit fyzickej model PZ, kterej bude fungovat. Nikdo to nedokáže.

Ověřit si to můžete sami
Představa, že se ve 21. století neví jistě, jakej tvar má Země (nebo že to ví jen pár lidí, a ti to “tají”), je směšná a odráží hlubokou nevědomost. Máme dostatečně pokročilou technologii a přehled o tom, co se děje kde na světě, abysme to lehko zjistili. A vůbec neni třeba lítat někam do vesmíru ani poslouchat nějaký autority. Základy toho, jak vypadá systém Země-slunce-měsíc-hvězdy, si můžete snadno dát dohromady sami. Stručně si to projdeme.
Kdokoliv si může spočítat, že slunce a měsíc jsou hodně daleko. (Viz dosvit, vždycky stejná velikost, viditelná jedna strana měsíce, atd.) Z toho, že kdekoliv na Zemi vychází a zapadá slunce za obzorem, viditelnym ve vzdálenosti malýho zlomku velikosti celý Země, je evidentní zakřivení na všech místech. Z toho, že slunce vždycky svítí na půl Země, je jasný, že je kulatá. (Kdyby Země byla placka, byl by z dalekýho slunce den a noc všude stejně.)
Z toho, že se pravidelně střídá noc a den, víme, že se buď Země točí, nebo slunce obíhá kolem nás (případně obojí). Zbejvá jen zjistit, která varianta je správná. To, že kolem nás všechno (slunce, měsíc, hvězdy) obíhá ve 24-hodinovym cyklu, je silná indikace točení Země. Jinak by muselo všechno obíhat kolem nás, každý podle vlastní trasy, která se mění v průběhu ročních období a delších cyklů.
Pozorování severního a jižního nebeskýho pólu a pohybu hvězd kolem nich nám už celkem jasně říká, že se Země točí a ukazuje nám, kde je její osa. Pokud by se Země netočila, muselo by každý těleso na obloze bejt specificky naprogramovaný, aby se chovalo konkrétním způsobem ve vztahu k Zemi, a něco by všechny ty pohyby muselo pohánět. Jelikož víme, že ty tělesa jsou daleko, varianta jejich obíhání (po neskutečně dlouhejch trasách za 24 hodin) nedává smysl, a to, že “obíhaji” všechny spolu, je jasná známka toho, že se Země ve skutečnosti točí. (Jinak by vlastně obíhal celej vesmír kolem Země, což je ale v podstatě to samý, jako že se Země točí.)
Tohle všechno se dá pochopit s použitím jen mozku a počítače, aniž byste vůbec museli vylejzat z domu. Nepotřebujeme NASA ani žádnou jinou autoritu. Dnes nám úplně stačí přístup k Internetu. (Ale chce to teda mít ten funkční mozek, což je poslední dobou trochu nedostatkový zboží.)
Kdo se tim bude chtít zabejvat víc a bude dlouhodobě sledovat oblohu a pohyb všech těles vůči Zemi a sobě navzájem, objeví cykly slunce, měsíce, atd. To už je o dost víc práce, ale máme 21. století a tohle všechno už za nás dávno někdo udělal, takže stačí si to jen ověřit. Náš model vesmíru nám spolehlivě předpovídá, kdy kde bude vidět slunce a měsíc, kdy budou zatmění, atd. To, že tyhle předpovědi vychází, nám ukazuje, že ten model celkem dobře funguje i v detailech.
Model PZ naopak nic takovýho ani předpovědět nedokáže, natož aby to vycházelo. Z modelu PZ se nedá předpovědět žádný zatmění a dokonce ani spočítat, odkud kdy bude vidět slunce. (V modelu PZ by slunce ve skutečnosti bylo vidět kdykoliv z celý Země a nebyl by tu ani den a noc.) Nedá se z něj ani předpovědět, kdy bude na kterym místě slunce zapadat. (Nemluvě o tom, že “zapadat” vůbec nemůže.)
Kdokoliv, komu to trochu myslí, si může vyzkoušet i pokročilejší experimenty. Ze vzdáleností na Zemi se například dá zjistit, jestli je plochá nebo zakřivená. Potřebujeme 4 místa ve slušnejch vzdálenostech od sebe, ideálně na úrovni moře. Takže si vezmeme trojúhelník Amsterdam – Petrohrad – Tripolis (Libye). Všechny města jsou u moře. Pak potřebujeme jedno někde uprostřed. Třeba Rijeka v Chorvatsku.
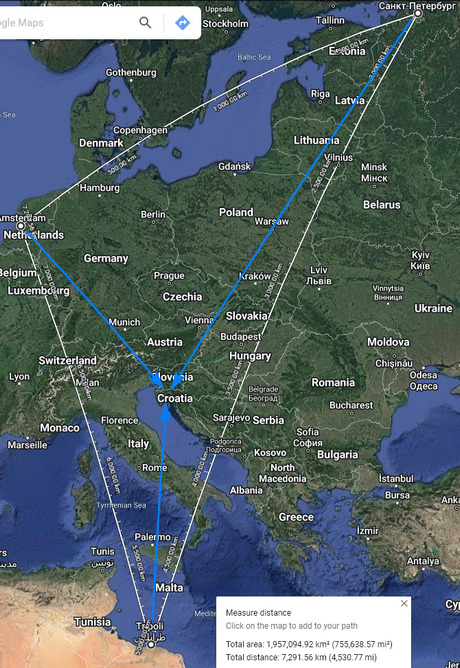
Zjistíme si vzdálenosti mezi prvníma třema městama a nakreslíme si ten trojúhelník na papír například v měřítku 1 mm = 10 km. Pak zjistíme vzdálenost Amsterdam-Rijeka, dáme do kružítka, zabodneme do Amsterdamu, nakreslíme kruh. Petrohrad-Rijeka, bodnout do Petrohradu, kruh. Tripolis-Rijeka, to samý. Pokud je Země plochá, musí se ty kruhy protnout v jednom bodě, protože všechny čtyři města jsou na úrovni moře. To se nestane. Vznikne jasnej trojúhelník. Potkalo by se to několik centimetrů nad papírem. Rijeka teda neni ve stejnej rovině jako ostatní tři města. Země neni plochá.
Vypočítat vzdálenosti slunce a měsíce už je těžší, ale i z laickýho hlediska se daji udělat nějaký odhady aspoň o realistickym rozmezí. I když nás nenapadne, jak změřit správný vzdálenosti, můžeme si nadhodit nějaký číslo a zjistit, co by to znamenalo. Co kdyby bylo slunce 100 000 km daleko? Fungovalo by to?
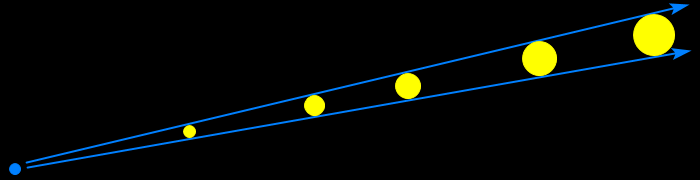
V první řadě, se vzdáleností jde ruku v ruce velikost. Slunce vidíme ze svýho pohledu nějak veliký a z toho vycházíme. Čím je dál, tím musí bejt větší, aby to odpovídalo tomu, co vidíme. Na obrázku je jednoduchej náčrt. Poměr vzdálenosti a průměru slunce je konstantní. V našem případě je to zhruba 108:1.
To znamená, že když si experimentálně hodíme slunce do vzdálenosti 100 000 km, nemůžeme mu dát libovolnou velikost. Bude mít zhruba 925 km v průměru. Pak si můžeme v první řadě spočítat, že takhle neosvítí 50% Země, ale jen asi 47%, což sice neni extrémní rozdíl, ale pořád dost velkej na to, abysme věděli, že to neodpovídá realitě – o 6% víc Země by mělo noc než den. S dnešní technologií si snadno ověříme, že to neodpovídá.
Druhá věc je, že slunce by bylo poloměrem 14x menší než Země a mělo by asi 2400x menší objem. V první řadě je teda jasný, že by Země nemohla obíhat kolem něj, ale muselo by slunce obíhat kolem ní. To na první pohled neni takovej problém, ale z dlouhodobejch složitějších astronomickejch pozorování by se to dalo vyvrátit.
Zároveň s tim tu ale máme tezi, že objekt 2400x menšího objemu než Země tu Zemi značně ohřívá na vzdálenost 100 000 km. To nezní pravděpodobně. Když si tohle všechno dáme dohromady, tak tenhle model neni realistickej – slunce je moc blízko a je moc malý, takže 100 000 km nám nestačí.
Z toho, jak jsou osvětlený měsíc a Země, vidíme, že vzdálenost ke slunci je mnohonásobně větší než k měsíci. Světlo slunce dopadá na Zemi skoro pod stejnym úhlem jako na měsíc. To je důležitej poznatek. Zároveň vidíme jen jednu stranu měsíce, což vyžaduje velkou vzdálenost pro měsíc.
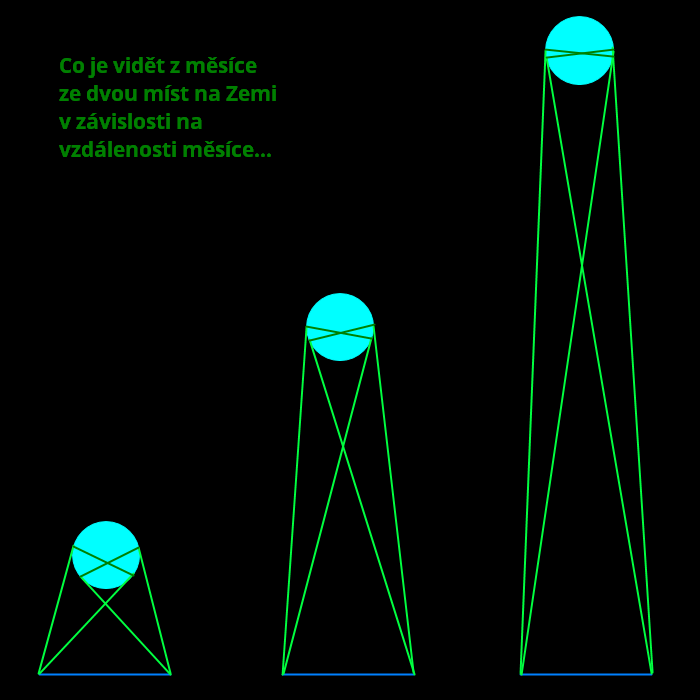
Když ze dvou míst na Zemi vzdálenejch 10 000 km od sebe vidíme stejnou stranu měsíce, musí ten měsíc bejt mnohonásobně dál než 10 000 km. O 100 000 km už by se tak nějak realisticky dalo uvažovat. A slunce musí bejt minimálně 10x, spíš tak 100x dál (než ten měsíc, o kterym jsme si teď vyjasnili, že je celkem daleko), protože jeho paprsky dopadaji na Zemi a měsíc pod skoro stejnym úhlem.

Ani jedno se teda rozhodně nepohybuje někde jen kousek nad Zemí. To je prostě fakt.
Zároveň je nepravděpodobný, že by slunce menší než Země zvládalo svoji roli (svítit na 50% Země a pořádně hřát). Jak daleko musí bejt slunce, aby bylo stejně velký jako Země? Víc než milión kilometrů (~1 370 000). I tak je ale nereálný, aby ohřálo Zemi. Takže milión km pro slunce se zdá pořád málo.
Aby slunce zahřálo Zemi, musí bejt masivní. (A kromě toho potřebuje dostatečnou zásobu energie, aby tu Zemi mohlo zahřívat miliardy let, což je při miniaturní velikosti těžko představitelný.) S velikostí nám sice narůstá i vzdálenost, ale objem s tou vzdáleností narůstá exponenciálně. Takže ve standardním modelu sice máme slunce 150 miliónů kilometrů daleko, ale objemově je víc než miliónkrát větší než Země.
Na milión km je slunce menší než Země, a na 10 miliónů km má objem asi 400x větší než Země. Tam už to trochu začíná dávat smysl. Ačkoliv dobrat se korektních výsledků je mnohem složitější, můžeme z běžnejch pozorování a jednoduchejch výpočtů dojít k tomu, že měsíc musí bejt tak aspoň sto tisíc km daleko, a slunce nejspíš aspoň desítky miliónů km. Pak máme k dispozici další data, jako třeba zatmění, z nichž zjistíme zase víc informací.
Experimentů se dá navrhnout a provést spousta. Představa, že takový věci nedokážeme spočítat, je absurdní. Lívanci si zjevně myslí, že tyhle věci nikdo neví jistě, protože všichni jen věří tomu, co jim někdo řek ve škole. Důvod, proč si tohle myslí, je očividnej: přesně v tejhle situaci byli oni sami. Věřili tomu, co jim bylo řečeno ve škole, aniž by něco z toho chápali.
Zádrhel je v tom, že si evidentně myslí, že všichni v tej škole byli tak hloupí, jako oni. Ve školách je ale vždycky určitý procento lidí, kteří o tom přemejšlí, pochopí to, a umí si to spočítat. Pro ně to potom neni víra na bázi indoktrinace, ale skutečný vědění. Lívanci, kteří nic z toho ve škole nepochopili, si nedokážou představit, že jiní žáci to pochopili.
Jak jsem tu ale ukázal, dát si tyhle věci dohromady neni nijak těžký a stačí k tomu vlastní pozorování a schopnost myslet. A v době Internetu, kdy si snadno můžeme dohledat milióny informací, je triviální si to všechno ověřit. Skutečnej tvar Země se nedá před lidma zatajit, protože mezi náma pořád existuje celkem dost lidí, kteří by na to přišli sami a nemusí se spolýhat na víru, jako lívanci.
Máme na Zemi dostatek lidí, kteří jsou mnohem chytřejší než já, a co mně zabere hodinu přemejšlení, kreslení a počítání, to oni vidí okamžitě. O to dál se pak dostanou, když tomu věnujou všechnu svoji energii. Kdyby lidstvo teď zapomnělo velikosti a vzdálenosti slunce a měsíce, tihle lidi by to dokázali dát dohromady během krátký doby s vysokou přesností.
Lívanci si to rozhodně sami dohromady nedaji. Ve škole byli indoktrinováni a nic z toho nechápali, což obvykle sami přiznávaji. Přesně proto se ale snadno nechaji indoktrinovat něčim jinym, protože to opět pořádně nechápou. Jen uvěřili, že jim tenkrát někdo lhal a že teď jim někdo jinej nelže.
Kdo umí počítat, přemejšlet a má prostorovou představivost, ten neni závislej na tom, komu se “rozhodne věřit”. Nepotřebuje věřit nikomu. Indoktrinace ho nezajímá. Prostě si to spočítá a ověří sám. V 21. století je to poměrně snadný.
Stínovej experiment
Čím víc si o tom tak přemejšlim, tím víc mě napadá způsobů, jak se dá ukázat, že “model” PZ je směšná hloupost. Stačí jen trochu se zamyslet a zvládat Pythagorovu větu a podobně.
Ukázali jsme si, že slunce na PZ je asi 5500 km vysoko a nejdelší možná vzdálenost, na kterou může svítit (aby mohla bejt nějaká noc), je asi 22000 km. Co z toho vyplývá? Poměr tý vzdálenosti a vejšky je 4:1. To znamená, že na PZ jakejkoliv stín může bejt maximálně 4x delší než je vejška toho, co ho vrhá. Jinými slovy, metr vysoká tyč, stojící na zemi, může na vodní hladině nebo vodorovnej zemi vrhat stín maximálně 4 metry.
To ale platí prakticky jen v Antarktidě, odkud jsou ty vzdálenosti nejdelší. ČR je na 50. rovnoběžce, takže tady ten poměr vychází následovně: rovnodennost 2x (stín dvojnásobek vejšky), letní slunovrat 1.6x, zimní slunovrat 2.4x. Neboli pokud je model PZ správnej, v ČR by metrová tyč u země nikdy neměla vrhat stín delší než 2.4 metru, a v létě by to nikdy nemělo dosáhnout ani 2 metrů. Model PZ víc nedovoluje.
Takže milí lívanci, běžte a udělejte si experiment. Zapíchněte někam metrovou tyč, aby vrhala stín na vodorovnou plochu, a měřte dýlku stínu při západu slunce. Jestli se dostanete na dva a půl metru, je to s vaší plochou Zemí dost v prdeli. Teď máme květen, tak byste se neměli dostat ani na 2 metry.
Tak šup! Je to jednoduchej experiment, kterej zvládne i opice.
 Hmm, z jakýpak je tohle asi planety?
Hmm, z jakýpak je tohle asi planety?
Stínovej experiment 2
Z předchozího experimentu mi nakonec vyplynul další, ještě o něco lepší. Je opět jednoduchej – může si ho snadno vyzkoušet kdokoliv, a ukáže nám jasně, kterej ze dvou modelů (koule/placka) je nesprávnej.
Stíny toho o trase slunce vypovídaji hodně. Na PZ má slunce obíhat v konstantní vejšce a přesně v kruhu. Vejšku měnit nemůže, protože to by žádnym způsobem nedávalo smysl, neboť by někomu klesalo na západě a někomu jinýmu v tu samou chvíli na východě, což by se nedalo nijak vysvětlit.
Že obíhá po kruhovej trase, je taky jasný, protože jakákoliv jiná trajektorie by opět do modelu vnesla ještě víc chaosu. O ničem z toho se, pokud vim, lívanci nepřou. A tenhle experiment má ještě tu výhodu, že je nám úplně jedno, v jakej vejšce se to slunce přesně nachází. Víme, že vejška je konstantní a dráha je kruh. (Ten kruh se sice v průběhu roku mění, ale v rámci 24 hodin je to kruh.)
Z toho nám vyplývá jednoduchej fakt: stín nějakýho předmětu, třeba kůlu zapíchnutýho v zemi, se musí taky pohybovat v kruhu. Ten kruh nebude mít střed tam, co je ten kůl (kromě na severním pólu), ale musí to bejt kruh. Musí tu existovat velká míra pravidelnosti, jak se dá lehko demonstrovat na tomhle obrázku:
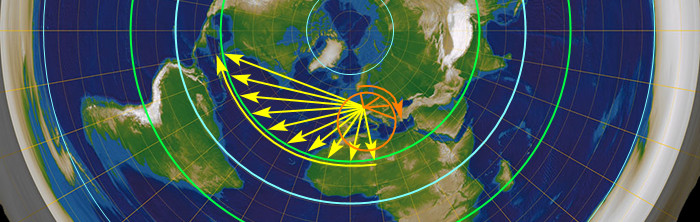
Budeme tu sledovat trasu slunce po obratníku Raka, tj. při letním slunovratu (ale funguje to i na druhym obratníku, rovníku, atd.). Jednak je trasa přesnej kruh, a jednak za stejnou dobu uběhne slunce vždycky stejnou vzdálenost. Tady nám žlutý šipky ukazujou polohu slunce na polednících. Poledníky jsou rozmístěný rovnoměrně, takže vzdálenost od jednoho ke druhýmu je vždycky stejná.
Jelikož tu máme 36 poledníků, cesta od jednoho ke druhýmu bude vždy 40 minut a vzdálenost bude vždy stejná. Pro experiment můžeme ale stejně tak použít hodiny – každou hodinu uběhne slunce stejnou vzdálenost po kruhovej dráze.
To zároveň znamená, že stín vrhanej kůlem v zemi se každou hodinu taky posune o stejnou vzdálenost. A taky musí opisovat přesnej kruh. To je prostě matematická nevyhnutelnost – když slunce běží v kruhu v rovině, která je rovnoběžná s rovinou, kam vrhá stín (plocha Země), musí stín taky opisovat kruh. Oranžově tu máme vyznačeno, jak se bude chovat ten stín. Jeho směr je vždycky prodloužením tý žlutý šipky, a jeho dýlka (oranžový rovný čáry) je úměrná dýlce tý žlutý šipky. Čím delší vzdálenost od slunce (žlutá šipka), tím delší stín (oranžová čára).
Na severním pólu si to představíme snadno, protože tam ten kůl bude ve středu toho kruhu. Na ostatních místech severně od obratníku nebude kůl ve středu, ale stín pořád musí kreslit přesnej kruh. To je významná skutečnost, protože nám to umožňuje provést experiment s jednoznačným výsledkem. Oranžově jsem protáh jen každou třetí šipku, ale vidíte, že i u těch “stínů” jsou ty rozestupy pravidelný a jdou v kruhu.
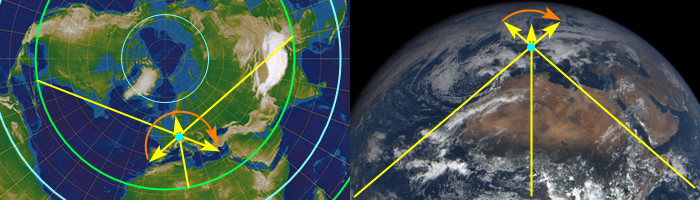
Třetí vlastnost toho stínu na PZ bude, že kolem kůlu opíše víc než 180°. Budeme experimentovat v ČR, takže severně od obratníku. Slunce začíná i končí trasu severně od místa pozorování, ale v poledne je na jihu. To znamená, že kolem kůlu opíše víc než 180°, a stejně tolik musí opsat i ten stín.
Pointa tohodle experimentu je, že na kulatej Zemi to všechno bude úplně jinak. Vzhledem k točení Země se stíny každou hodinu pohnou o jinou vzdálenost. Jak už bylo vidět v předchozím experimentu, při východu a západu slunce se bude stín za stejnou dobu pohybovat o mnohem větší vzdálenosti než kolem poledne, protože slunce z našeho pohledu neni ve stejnej vejšce, ale blíží se k obzoru, takže se značně mění úhel, pod kterym na nás dopadá světlo.
Zároveň trasa stínu nebude opisovat přesnej kruh, a k tomu opíše míň než 180° kolem kůlu, protože sluce je celej den jižně od místa pozorování (nicméně tohle je trochu složitější). Tenhle experiment nám teda jasně ukáže, kterej model je špatně, protože oběma odpovídat nemůže.
S těma 180° to platí, když je slunce na rovníku nebo níž (jižně od něj). Když je na obratníku Raka, tak to těch 180° přesáhnout může, protože kulatá rotující Země s osou nakloněnou vůči ekliptice je trochu záludná:
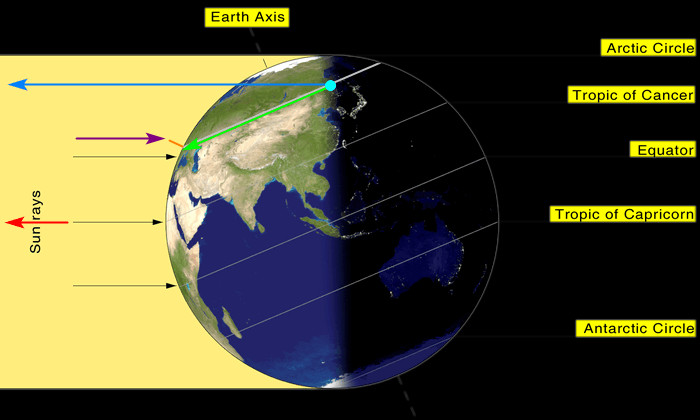
Modrá tečka ukazuje místo na naší zeměpisnej šířce při západu slunce při letním slunovratu. Světlo slunce dopadá kolmo na obratník Raka. Červená šipka ukazuje směr, kde je opravdu slunce. Modrá šipka ukazuje, kde uvidíme večer slunce my. A zelená ukazuje, kde máme západ. Takže jelikož je severní pól natočenej trochu ke slunci, uvidíme slunce trochu na sever.
Oranžová čára je, kde budeme v poledne. Na obratníku lidi uvidí slunce přímo nad sebou. My ho díky zakřivení Země uvidíme na jihu. Fialová šipka ukazuje, jak na nás bude dopadat světlo, a oranžová čára má směr někoho stojícího na Zemi – kolmo k povrchu. Stín půjde na sever, zatímco při západu se bude od východního směru stáčet trochu na jih.
Experiment teda můžeme provést tak, že do země zapíchneme kůl a každou hodinu zapíchneme kolík tam, kam nám dopadne špička stínu. Samozřejmě potřebujeme rovnej terén, protože svah by to zkresloval. Alternativa je vzít nějakou vodorovnou desku, na ni postavit něco, co bude vrhat stín (baterku, láhev, svíčku…), a každou hodinu dělat na desce značky, kam dopadá stín. Ideální by bylo sledování celej den, ale stačí nám doba mezi polednem a buď západem nebo východem slunce. Doba kolem východu/západu bude ukazovat nejvýraznější rozdíly mezi modely koule a placky, takže ta je nejzásadnější.
Máme teda jasně daný, co můžeme od kterýho modelu očekávat. Na PZ musíme vidět tohle:
1. Rozestupy mezi kolíky budou všechny stejný.
2. Trasa stínu bude opisovat přesnej kruh.
3. Stín kolem kůlu opíše víc než 180°.
Na zeměkouli oproti tomu uvidíme tohle:
1. Rozestupy mezi kolíky budou ráno a večer větší než v poledne.
2. Trasa stínu nebude opisovat přesnej kruh.
3. Stín kolem kůlu opíše míň než 180° (od podzimu do jara).
Je to velice jednoduchej experiment, kterej zvládne kdokoliv. Neřekne nám nutně, jestli je jeden model správnej (konzistence s modelem ještě neznamená, že je správnej celej model), ale rozhodně nám řekne, jestli je jeden z nich nesprávnej.
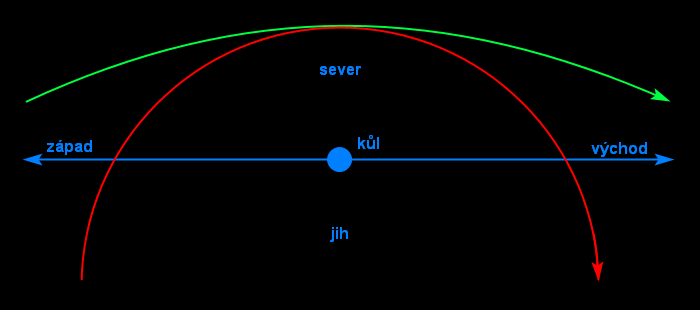
Tady vidíme náčrt předpovědí pro oba modely. Na kouli se stín bude pohybovat zhruba podle zelený šipky. Na PZ by měl začínat a končit pod modrou čarou a opisovat přesně kruhovou trasu, se středem jižně od kůlu. O něco složitější je z laickýho hlediska odhadnout, jestli ta zelená šipka bude zatáčet nahoru nebo dolu (nebo bude rovná).
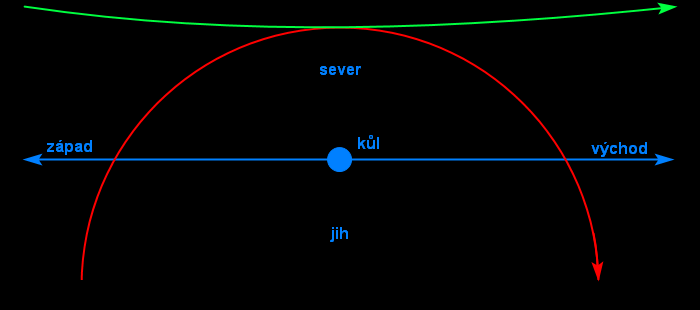
Se sluncem na rovníku by měl bejt správnější druhej obrázek, ale se sluncem na obratníku Raka to bude ten první a ještě ta šipka překříží tu modrou čáru – ale ne o tolik, jako ta červená. V nějakym období mezi tim by ta zelená čára asi měla jít rovně. Přesná trasa zelený šipky je těžko předvídatelná (na rozdíl od červený), ale podstatný je, že od podzimu do jara by se ten stín neměl dostat na jih od kůlu (pod modrou čáru), zatímco na PZ by se tam dostat naopak měl bez ohledu na roční období.
V létě se tam dostane i na kouli, ale ráno a večer se bude zkracovat/prodlužovat mnohem rychlejc než kolem poledne a stín nebude kreslit přesnej kruh (kromě na pólu).
Až se poštěstí mít volnej den bez mraků, můžete si to vyzkoušet. Když se to nepodaří trasovat celej den, odpadne nám bod číslo 3, ale ty první dva nám pořád stačí. Nejzásadnější je ten rozdíl mezi polednem a západem nebo východem slunce. Nicméně pro bod 3 nám zase stačí jen 3 pozorování (v zimní polovině roku) – brzo ráno, kolem poledne, a pozdě večer, a to samo o sobě by taky vypovídalo hodně.
Proved jsem několik vlastních experimentů. Výsledky najdete tady.
Jak operujou lívanci
Při svejch interakcích s lívancema jsem zjistil, že všichni jedou podle stejný šablony:
– umí kritizovat kulatou Zemi
– neumí vysvětlit, jak funguje plochá Země
– nedokážou odpovědět na moje otázky
– prakticky neposlouchaji nic, co jim říkám
Typickej aspekt interakce s lívancem je ten, že po vás chtěji vysvětlit, jak něco funguje na zeměkouli (přičemž neni moc jasný, proč si to během 5 minut nezjistili sami na Internetu), vy jim to vysvětlíte, oni vás ignorujou a zeptaji se, “a jak funguje tohle?” a pokračujou s další hloupou otázkou. Donekonečna.
Zajímavá ironie je, že všichni naprosto stejně melou o tom, že já jsem indoktrinovanej a nikdy jsem o tom nepřemejšlel (jak ví, o čem jsem přemejšlel nebo nepřemejšlel, mi neobjasnili, ale nevadí), a přitom je evidentní, že jsou indoktrinovaní oni a soudě podle některejch těch otázek, co jsme tu viděli, neni moc jistý, že o tom opravdu přemejšleli oni.
Všichni blábolí stejný nesmysly, který maji ze stejnejch videí na youtube, a kterejm ve většině případů ani nerozumí. Všichni vytahujou earthcurvature.com, ale nikdo z nich nechápe, že ty výpočty fungujou jen na planetě bez atmosféry. Všechny svoje “experimenty” dělaji bez tohodle vědomí.
Všichni papouškujou stejný blbosti, jejichž smysl ani nechápou, jako že “paprsky slunce by měly bejt rovnoběžný” nebo že “odraz na hladině je po celej dýlce od horizontu až k pozorovateli”. Papouškujou otázky jako “Proč vidíme celej rok stejný hvězdy?” bez vědomí, že to ani neni pravda. A přitom se tváří, že jsou s vědomostma před ostatníma lidma napřed.
Už jenom to, že všichni jako podle šablony vytahujou, jak jsme my ostatní indoktrinovaní, svědčí o jejich indoktrinaci. To je koneckonců starej trik, říct lidem, “Byli jste indoktrinovaní! Vymyli vám mozky! Teď poslouchejte!”, a vymejt jim mozek něčim jinym. Což dělaji všechny ty jejich přihlouplý videa. A oni pak jdou a jako na povel všem melounům říkaji, jak jsou “indoktrinovaní”.
Původně jsem se o tohle téma začal zajímat s pocitem, že lívanci jsou inteligentní. Týhle iluze mě ale v posledních tejdnech bohužel dost zbavili oni sami. Jsou mezi nima samozřejmě rozdíly, ale mnozí svejma nevědomostma a neschopností myslet překonávaji zombíky. Ale pořád jim dávám šanci. Když mi vysvětlí z pohledu PZ těch 10 bodů, co jsem tu napsal, klidně se nechám přesvědčit, že Země je plochá.
Oni sami bohužel často reagujou tvrzením, že si můj článek ani nepřečetli, ale nic je nemůže přesvědčit, že Země je kulatá. Mě by důkazy přesvědčily, že je plochá. Jestli někteří z nich už předem ví, že je nic nepřesvědčí, tak je evidentní, že je nezajímá pravda, ale utvrzení se ve svojí víře.
Kolikrát po mně ještě hážou nesmysly, že jsem se nechal oblbnout institucema jako NASA. Což je vtipný, protože jsem nikde nic od NASA nepoužil a leta tvrdim, že NASA je banda lhářů. Proč mi tohle předhazujou? Na čem to založili? Na ničem. Je to jejich indoktrinace. Na youtube je naučili říkat lidem, že “uvěřili NASA”. Že jsem nic ze svejch argumentů nezaložil na ničem, co má na svědomí NASA, je jedno.
Obviňovat se z indoktrinace klidně můžeme všichni navzájem, ale na tom nezáleží. Podstatný je dokázat svoje tvrzení vysvětlit. Já to dělám. Lívanci mi nebyli schopni vysvětlit nic. Indoktrinace je opakování věcí, který nechápete. Já na rozdíl od lívanců chápu, co říkám. Dokud oni nezvládnou vysvětlit, jak ten jejich nemodel funguje (na což pořád marně čekám), nemínim na ně plejtvat dalším časem.
Psychologická operace “Plochá Země”
Jak je možný, že je tahle hovadina tak rozšířená a ještě získává víc příznivců, když je úplně jednoduchý dokázat mnoha způsoby, že je to blbost? Je možný, že lidi začnou samovolně věřit něčemu, co evidentně nedává smysl? Neni to pravděpodobný.
Hromadná víra v nesmysly obvykle nastává jen tehdy, když se o to někdo snaží. Podle všeho se někdo hodně snaží přesvědčit co nejvíc lidí v alternativě, že Země je plochá. To by samozřejmě nebylo ani trochu překvapivý a důvod se jasně nabízí.
Stačí se podívat na to, jakej to má důsledek a zeptat se, Qui bono? Je evidentní, že víra v PZ lidi snadno diskredituje, když mluví o jinejch věcech. Žádnej lívanec nemá šanci prosadit cokoliv v mainstreamu, protože médiím stačí říct lidem “lol, on věří, že Země je plochá”, a nikdo ho nebude brát vážně. Je to běžnej trik, kterej parádně funguje.
Můžeme se obviňovat navzájem – já můžu tvrdit, že lívanci si nechali vymejt mozek a stali se obětí konspirace, a oni můžou tvrdit to samý o mně. To samo o sobě nemá žádnou váhu. Dokud konspiraci nedokážeme, jsou to jen tvrzení. Má to ale dva háčky.
Za prvý, já jsem právě vysvětlil, jakej má smysl nakukávat lidem, že Země je plochá. Je to perfektní PsyOp. To, jakej má smysl nakukávat lidem, že Země je kulatá, jestli je ve skutečnosti plochá, jsem pořád moc nepochopil. Ani jak do tý konspirace zatáhnout úplně absurdní množství lidí, aniž by se našel aspoň jeden whistleblower ze všech těch oborů, který pracujou s konceptem kulatý Země, kterej je údajně mylnej. Jak všechny tyhle obory fungujou, je taky záhada.
Za druhý, kde je nebo neni jaká konspirace, neni nijak důležitý. Důležitý je, že tvar Země a vzdálenost slunce, měsíce, atd. se dá snadno dokázat, a všechno to dokázáno bylo moha způsoby, z nichž si spoustu může kdokoliv vyzkoušet sám, jak jsem tady ukázal. Pokud chce někdo všechny tyhle experimenty a důkazy ignorovat a tvrdit dál evidentně nepravdivý věci, je to jeho právo.
Tímto téma “plochá Země” uzavírám do tý doby, než mi někdo ukáže, jak na PZ funguje světlo, západ slunce, vzdálenosti, oběh hvězd, jedna viditelná strana měsíce, a taky jakej je dohled lidskýho oka.